Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 30

9.2 Общие сведения и основные понятия цифровой интерполяции сигналов с целочисленными коэффициентами

В ЦОС под термином интерполяция подразумевается процесс ЦОС, приводящий к формированию сигнала  с повышенной частотой дискретизации из сигнала  с более низкой частотой дискретизации при определенных ограничениях на временные и спектральные изменения исходного сигнала. Т.о. новый интервал дискретизации равен 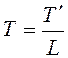;  – прежний интервал дискретизации.

Можно выделить три разновидности процесса интерполяции при ЦОС:

1.  Увеличение частоты дискретизации осуществляется в соответствии с математическим понятием интерполяции. В этом случае в исходных точках отсчетов  или  отсчеты новой и старой функции совпадают:

.

Т.е. если исходная функция  содержала  отсчет, то полученная функция  содержит  отсчет (между каждой парой отсчетов  добавляется еще несколько отсчетов .

2.  При увеличении частоты дискретизации исходные отсчеты дискретного сигнала  оказываются утерянными, однако отсчеты выходного сигнала  могут рассматриваться как отсчеты исходного аналогового сигнала  из которого путем дискретизации с интервалом  был образован исходный дискретный сигнал . В этом случае огибающая сигналов  и , а так же их спектр – не изменяются.

3.  Увеличение частоты дискретизации приводит к изменению формы интерполируемого сигнала, однако модуль его спектра не изменяется.

Во всех случаях процесс преобразования описывается структурной схемой (рисунок 9.1).

Входной аналоговый сигнал  поступает на идеальный дискретизатор Д, работающий с интервалом дискретизации  (L – целое число). Выходной дискретный сигнал ,  поступает на идеальный интерполятор ИИ, увеличивающий частоту дискретизации в L раз. Таким образом, сигнал  можно рассматривать как результат дискретизации исходного аналогового сигнала  с интервалом дискретизации 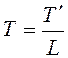. Выходной сигнал системы ,  получается в результате преобразования выходного сигнала ИИ  линейной дискретной системой с частотной характеристикой

                                         (9.1)

Иными словами АЧХ системы , т.е. форма модуля спектра не изменяется, а ФЧХ  для разных случаев может быть разной.

Для случая 1: Дискретная система  обладает линейной ФЧХ, т.е.  – целое число, не зависит от частоты, ФЧХ имеет вид:

 (линейно зависит от частоты).

Для случая 2: дискретная система  обладает линейной ФЧХ: , т.е. , но  – нецелое число.

Случай 3: Дискретная система  обладает нелинейной ФЧХ, т.е.  – зависит от частоты; в этом случае огибающая сигнала  не является отсчетами сигнала , но модуль спектра сигнала  в основной полосе частот по прежнему имеет тот же вид, что и модуль спектра входного сигнала , поэтому по дискретному сигналу  может быть восстановлен аналоговый сигнал , модуль спектра которого совпадает с модулем спектра исходного сигнала , т.е. информация не будет утеряна.

Рассмотрим теперь частотную интерпретацию процесса интерполяции цифрового сигнала с целочисленным коэффициентом L = 3.

Пусть спектр исходного сигнала  имеет вид, изображенный на рисунке 9.2,а.

После дискретизации исходного сигнала с частотой дискретизации 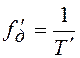 модуль спектра  имеет вид, изображенный на рисунке 9.2,б. При дискретизации же с частотой в три раза выше,  или 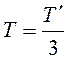 получим модуль спектра  дискретизированного сигнала  (рисунок 9.2,в).

Отличие между этими спектрами состоит в том, что (не считая амплитуды) в спектре  имеются “лишние” частотные составляющие с центральными частотами  и . Таким образом, процесс повышения частоты дискретизации сигнала  эквивалентен преобразованию спектра сигнала от вида 9.2,б к виду 9.2,в, т.е. к подавлению “лишних” частотных составляющих исходного спектра с помощью цифрового фильтра.

9.3 Эспандер частоты

Мы уже уяснили, что процесс интерполяции осуществляется путем цифровой фильтрации с целью подавления “лишних” составляющих спектра. Однако цифровой фильтр работает на определенной частоте дискретизации. Следовательно, перед цифровой фильтрацией сигнала необходимо осуществить предварительное увеличение частоты дискретизации исходного