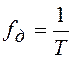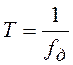Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 3

; .                                         (1.1)

Чем выше , тем труднее вычислителю выполнить большое количество операций над отсчетами в темпе их поступления на переработку, и тем сложнее должно быть его устройство. Таким образом, точность представления сигнала требует увеличить , а стремление сделать вычислитель как можно более простым приводит к желанию понизить .

Однако существует ограничение на минимальное значение : для полного восстановления непрерывного сигнала  по его отсчетам  необходимо и достаточно, чтобы частота дискретизации  была, как минимум, в два раза больше наивысшей частоты  в спектре передаваемого сигнала , т.е.

                                                  (1.2)

Соотношение (1.2) получило название теоремы Котельникова.

Реальные сигналы ограничены во времени, поэтому их спектр бесконечен (рисунок 1.2,б). Отсюда следует, что при  дискретизация невозможна. Тем не менее, в спектре любого конечного сигнала есть такие частоты, которые, начиная с некоторой  имеют незначительные амплитуды, и поэтому ими можно пренебречь без заметного искажения самого сигнала. Значения  определяется конкретным типом сигнала и решаемой задачи. Например, для стандартного телефонного сигнала  кГц. Минимальная стандартная частота его дискретизации  кГц. Ограничение спектра до частоты  осуществляется аналоговым ФНЧ, получившем название антиэлайсингового. Сигнал и его спектр на выходе ФНЧ изображены на рисунке 1.2,в).

Квантование отсчетов по уровням (или квантование) производится с целью формирования последовательности чисел: весь диапазон изменения величины отсчетов разбивается на некоторое количество дискретных уровней N, и каждому отсчету по определенному правилу присваивается значение одного из двух ближайших уровней квантования, между которыми оказался данный отсчет (рисунок 1.2). В результате получается последовательность чисел , представляемых в двоичном коде. Количество уровней определяется разрядностью п АЦП; так если п = 3, то всего можно иметь  уровней квантования, а минимальное и максимальное значения отсчетов соответственно  и . Ясно, что квантованный отсчет отличается от выборки . Это отличие является ошибкой квантования

,                                     (1.3)

которое теме больше, чем меньше п. Максимальная ошибка квантования равна половине шага квантования .

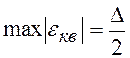, где                                    (1.4)

Отсюда следует, что чем больше разрядность АЦП, тем точнее представляется отсчет и тем сложнее и дороже оказывается АЦП. Современные АЦП имеют разрядность от 8 до 20.

Последовательность  поступает на вычислитель, который по заданному алгоритму каждому отсчету  ставит в однозначное соответствие выходной отсчет

.

Результатом обработки исходного сигнала является новая цифровая последовательность – цифровой сигнал  (рисунок 1.2,ж), существенно отличающийся от . Количество операций (умножений, сложений, пересылок и т.д.) для получения одного отсчета  может исчисляться тысячами, поэтому вычислитель должен работать на более высокой тактовой

Рисунок 1.2

частоте , чем , чтобы успеть произвести все необходимые действия до поступления очередного отсчета , т.е. какой бы сложности не был алгоритм, время переработки  не должно превышать периода дискретизации

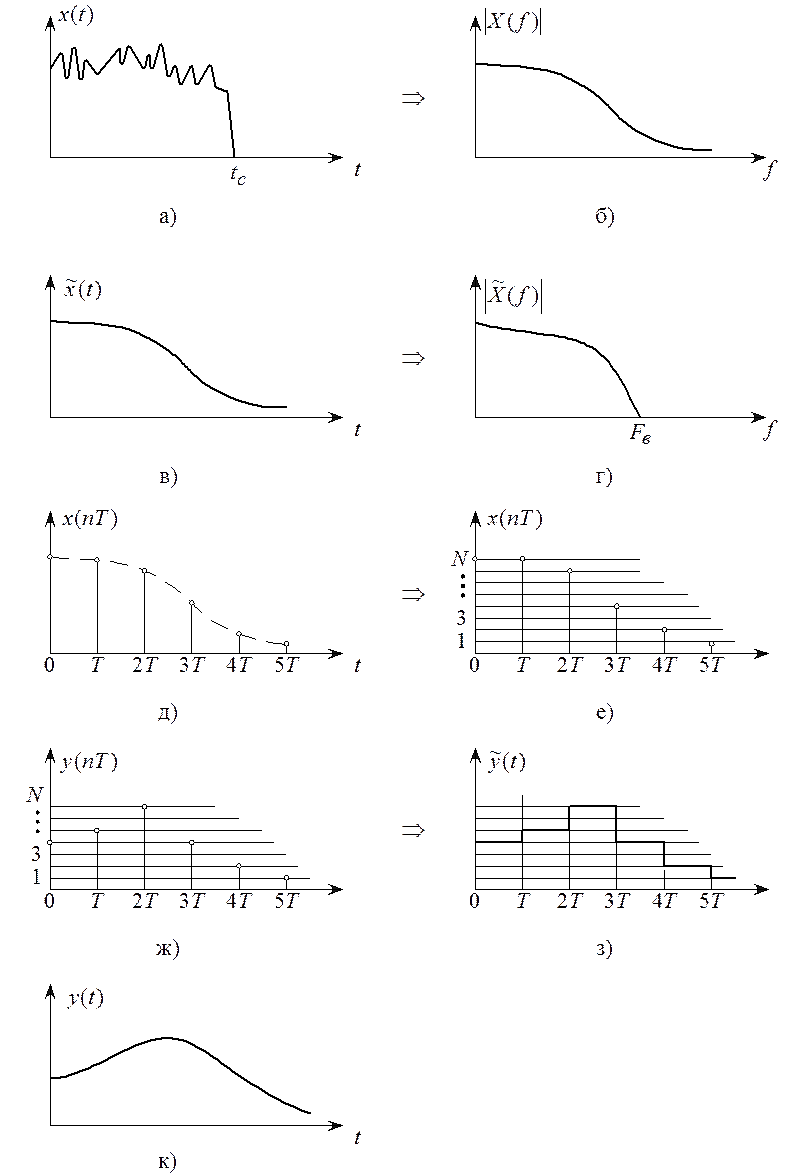
Именно при этих условиях возможна работа вычислителя в реальном масштабе времени, т.е. в темпе поступления входных отсчетов. Например, при обработке стандартного телефонного сигнала с  кГц для обеспечения работы вычислителя в реальном масштабе времени тактовая частота должна быть по крайней мере 6 МГц, как в процессорах первого поколения TMS320C10. Полученные выходные отсчеты подаются на цифро-аналоговый преобразователь (ЦАП), формирующий ступенчатый сигнал  – (рисунок 1.2,з) который затем с помощью сглаживающего фильтра НЧ преобразуется в аналоговый поперечный сигнал  (рисунок 1.2,ж).