Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 25

-  модуль отсчета входного сигнала . Это достигается масштабированием входного сигнала;

-  фильтр реализуется в прямой форме;

-  числа представлены в форме с фиксированной запятой или дополнительном коде;

-  каждое произведение округляется.

Целью расчета разрядности регистров оперативной памяти является определение разрядности  дробной части кода входного сигнала. Поскольку абсолютная величина отсчетов входного сигнала нормирована так, что , то разрядность кода целой части равна нулю. Также необходимо рассчитать разрядности  и  тех частей регистра выходного сигнала , в которых фиксируются целая и дробная части кода выходного сигнала .

Расчет величины

Поскольку выполняется условие  и , то

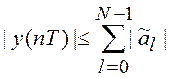,                                         (7.3)

откуда

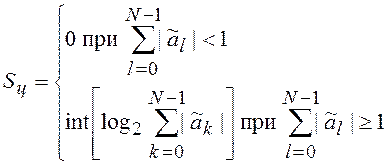                        (7.4)

Условие (7.4) гарантирует отсутствие переполнения регистра входного сигнала.

Расчет величины  и

Здесь существуют разные подходы к определению  и .

Вероятностный подход. Пусть задана величина  – допустимая дисперсия (средняя мощность) шума на выходе фильтра, причем этот шум обусловлен шумами округления отсчетов выходного сигнала фильтра и, возможно, каждого произведения при вычислении отсчетов выходного сигнала.

Известно, что дисперсия шума округления входного сигнала  связана с разрядностью  следующей зависимостью:

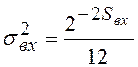                                             (7.5)

Если все произведения вычисляются точно (т.е. отсутствуют собственные шумы фильтра), то дисперсия шума на выходе  равна

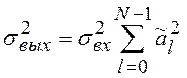                                         (7.6)

т.е. дисперсия шума на выходе фильтра определяется лишь дисперсией шума округления входного сигнала и коэффициентов фильтра.

Из (7.5) и (7.6) получим:

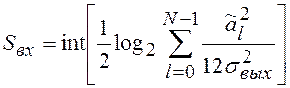                                        (7.7)

Очевидно, что собственные шумы фильтра отсутствуют при

                                           (7.8)

Если вычисления выполняются с округлением после каждой операции умножения до  двоичных разрядов, т.е. присутствуют шумы округления , то

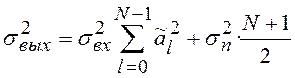,                              (7.9)

где 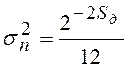 – дисперсия шума округления. Мощность собственных шумов фильтра 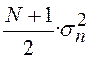 должна быть мала по сравнению с мощностью шума входного сигнала. Можно принять, примерно, что

.

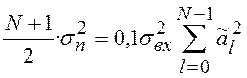Из двух последних выражений следуют формулы для расчета разрядности регистров выходного сигнала:

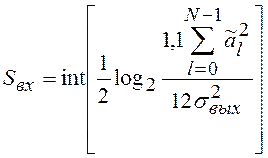                                   (7.10)

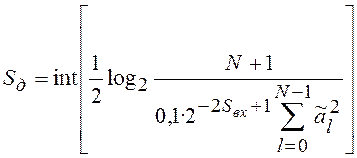                          (7.11)

Расчет величин  и  на “худший случай”

Пусть задана максимальная абсолютная погрешность  отсчетов выходного сигнала

, где  – отсчеты выходного сигнала “точного” фильтра, в котором все операции выполняются точно и на вход которого подается “точный” выходной сигнал;

 – отсчеты выходного сигнала фильтра с теми же коэффициентами, на выход которого подается округленный до  разрядов входной сигнал и, возможно, все произведения выполняются с округлениями до  разрядов.

Если все произведения выполняются точно и , то

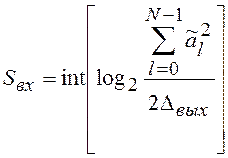                                    (7.12)

.                                           (7.13)

Если произведения выполняются с округлением, то

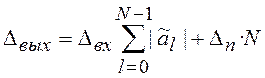,                               (7.13)

где  – погрешность отсчетов входного сигнала, определяется округлением этих отсчетов до  разрядов. Она равна половине шага квантования входного сигнала;

 – погрешность отсчетов выходного сигнала, определяемая округлением произведений.

Чтобы фильтр не вносил значительных дополнительных погрешностей за счет шумов округлений произведений в значения отсчетов выходного сигнала, по аналогии с предыдущим случаем принимается

.

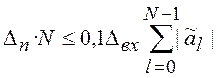В результате получаются расчетные формулы:

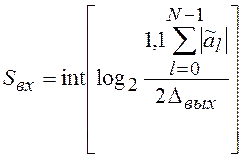                               (7.14)

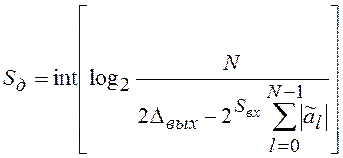                               (7.14)

7.4 Алгоритм роста разрядности коэффициентов фильтра, реализуемого на специальном микропроцессоре