Цифровая обработка сигналов. Основные понятия и определения. Сигналы и их спектральное представление, страница 15

Применив Z-преобразование к (5.4) и решив его относительно , найдем передаточную функцию рекурсивного ЦФ

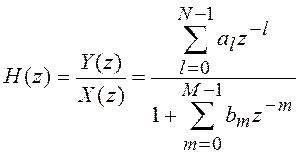                                (5.5)

Рассмотрим некоторые, наиболее часто используемые структурные схема рекурсивных ЦФ.

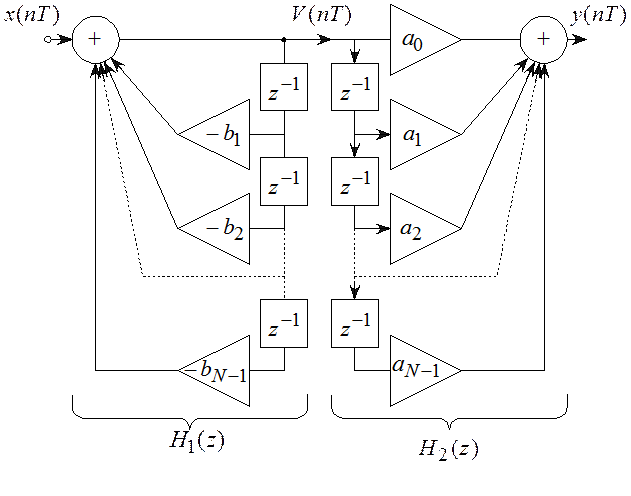
Прямая форма реализуется непосредственно по его разностному уравнению (5.4) или по передаточной функции (5.5). Она содержит один сумматор, умножители и  элемента задержки (для создания цепей, соответствующих числителю и знаменателю передаточной функции  используются отдельные элементы задержки). Порядок фильтра определяется высшим порядком полиномов числителя или знаменателя.

Пример 5.3 Биквадратный блок (ББ) – фильтр второго порядка описывается разностным уравнением

или, соответственно, передаточной функцией:

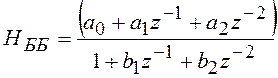.                             (5.6)

Изобразим структурную схему этого блока.

Рисунок 5.6

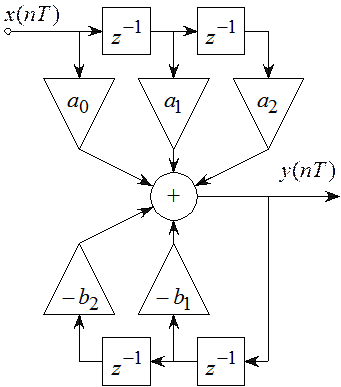
Прямая форма структуры ББ содержит сумматор и 4 элемента задержки (рисунок 5.6).

Недостаток такого способа реализации – сравнительно большое число ячеек памяти, применяемой для рекурсивной и нерекурсивной частей. Уменьшить число этих ячеек позволяют каноническая (в смысле оптимального решения) схема, в которой каждый элемент задержки используется для цепей как нерекурсивной, так и рекурсивной частей схемы.

Прямая каноническая форма. Канонической называют структурную схему фильтра, содержащую минимальное число элементов задержки. Домножив числитель и знаменатель (5.5) на некоторую функцию , передаточную функцию рекурсивного ЦФ (5.5) можно представить в виде

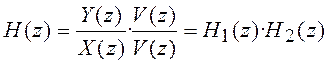
где

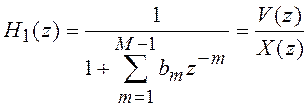 и .

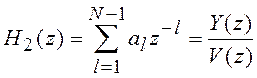Передаточным функциям  и  соответствуют разностные уравнения

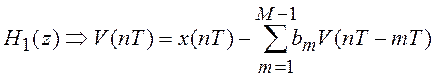                  (5.7)

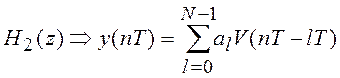                        (5.8)

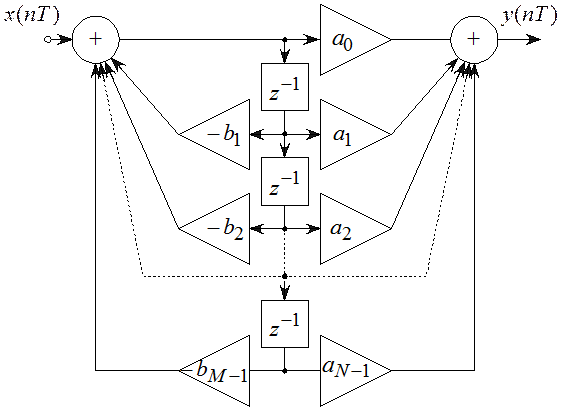
Алгоритм (5.8) определяет структуру построения нерекурсивного ЦФ, у которого входным сигналом является сигнал , а (5.7) рекурсивного ЦФ, у которого выходным сигналом является сигнал . Т.о. общая схема рекурсивного ЦФ включает в свою структуру 2 части – рекурсивную и нерекурсивную (рисунок 5.7).

Рисунок 5.7

Т.к. в фильтрах, реализующих  и  имеет место задержка только сигнала , то дублирующие элементы задержки можно объединить и использовать только один набор элементов задержки (рисунок 5.8).

Прямая каноническая схема содержит минимальное число L элементов задержки:  и два сумматора.

Рисунок 5.8

Рисунок 5.9

 

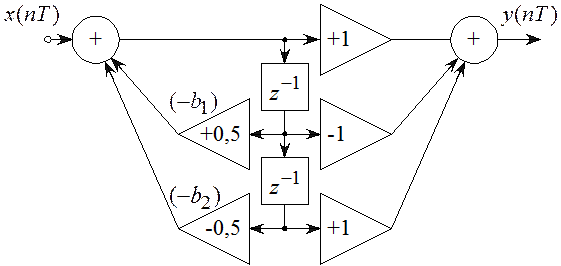
В качестве примера приведем прямую каноническую форму структурной схемы ББ (рисунок 5.9) с передаточной функцией вида

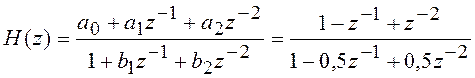, здесь .

Пример 5.4 Рассчитать сигнал на выходе дискретной цепи, имеющей передаточную функцию 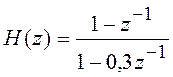, если дискретный сигнал на входе цепи задан отсчетами .

Структурная схема цепи изображена на рисунке 5.7.

Воспользуемся выражением (5.4) (разностным уравнением).

;

;

;

;

Рисунок 5.10

;

;

;

;

…

и т.д.

Пример 5.5 Найдем реакцию дискретной цепи на воздействие  если передаточная функция цепи имеет вид

.

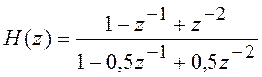Найдем выходной сигнал, используя разностное уравнение (5.4)

.

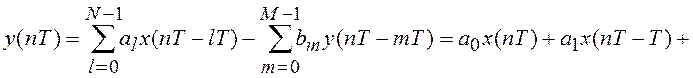
Рассчитаем отсчеты

 т.к.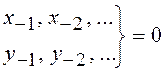

;

и т.д.

Вывод: количество отсчетов на выходе рекурсивного ЦФ теоретически бесконечно. Со временем отсчеты уменьшаются по синусоиде и постепенно стремятся к нулю.

Каскадная (последовательная) форма реализации рекурсивных фильтров является одной из наиболее часто применяемых схем реализации ЦФ высоких порядков и соответствует представлению передаточной функции  в виде произведения

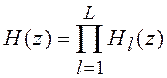,                                           (5.9)

где  – передаточная функция биквадратного блока:

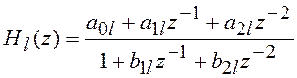,                          (5.10)