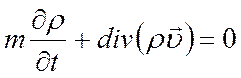Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 6

                                              .                                   (5)

          Для стационарной фильтрации сжимаемого флюида:

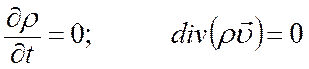                                                                         (6)

Если сжимаемостью флюида можно пренебречь:          

,                то уравнение  (6) приводится к виду:

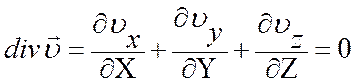                                 .                              (7)

2.  Дифференциальное уравнение движения.

        Дифференциальное уравнение движения флюида в пористой среде  является обобщением закона фильтрации Дарси:

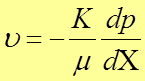                                                 .                                                  (8)

 ---- пространственная производная давления ( в направлении оси Х).

          Вектор пространственной производной в направлении максимальной скорости изменения функции  --- это градиент:

.

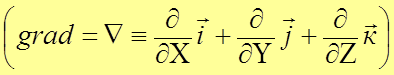Т.о.  в векторной форме закон фильтрации Дарси записывается в виде:

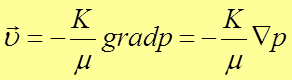                                            .                            (9)

          В подземной гидромеханике используется специальная функция:

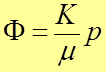                                                             .                                      (10)

Функция      называется   потенциалом скорости фильтрации.

          Если кроме давления действуют другие силы (например, сила тяжести), то потенциал скорости фильтрации):

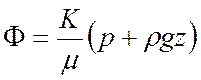                                                                                    (10а)

          Таким образом закон фильтрации Дарси можно записать в обобщенной форме:

                                                  .                          (11)

          Из уравнения неразрывности (4) и закона фильтрации (11) можно получить уравнение движения флюида в пористой среде:

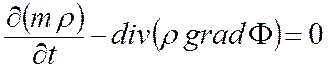                                           ;                        (12)

или

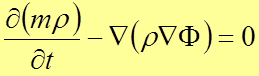                                                 .                              (13)

          В подробной (координатной) записи уравнение (13) имеет вид:

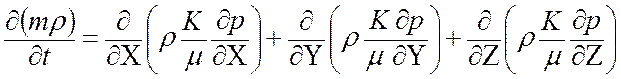             .      (14)

          Для решения дифференциального уравнения движения (13) необходимо иметь начальные и граничные условия.

          Начальные условия заключаются в задании искомой функции во всей области в некоторый начальный момент времени (например, значения давления в пласте до начала разработки).

          Граничные условия задаются на границах пласта: на внешней границе и на внутренней границе (на забое скважины).

          Закон Дарси (11) и соответствующее ему дифференциальное уравнение движения (13) пригодны для изотропной пористой среды, т.е. среды, проницаемость которой во всех направлениях одинакова.

          На практике часто встречаются пористые среды, проницаемость которых различна в разных направлениях (например, осадочные пласты с отчетливой слоистой структурой). Пористые среды, в которых коэффициент проницаемости зависит от направления потока, называются анизотропными.

          Для анизотропных пористых сред закон фильтрации (и соответственно, уравнение движения) имеют более сложный вид, чем выражения (9) или (14), т.к. векторы скорости фильтрации и градиента давления не совпадают по направлению.

          Для анизотропных пористых сред закон Дарси и уравнение движения записываются в тензорной форме:

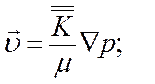                                                                                              (15)

 - тензор проницаемости пористой среды:

              ;

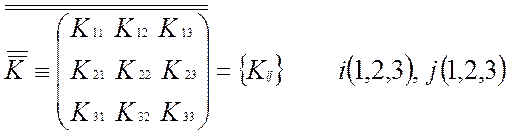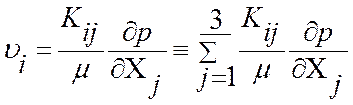                                         .                    (16)

          Анизотропия естественных осадочных пород – коллекторов обусловлена их отчетливой слоистой структурой. Фильтрационные свойства таких пород одинаковы в направлениях, лежащих в плоскости слоя, но изменяются в перпендикулярном направлении.

          В данном случае систему координат выбирают таким образом, чтобы плоскость XY лежала в плоскости слоя, а ось Z была перпендикулярна слою. Выбранные таким образом оси координат называются главными осями пласта. Закон Дарси  в этом случае можно записать в виде:

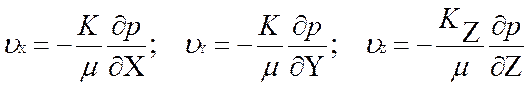                  .             (17)