а) Уравнение неразрывности фаз.
Рассмотрим конечный
неизменный объём пористой среды ![]() , ограниченный
поверхностью
, ограниченный
поверхностью ![]() . Объём порового пространства V
. Объём порового пространства V![]() ; насыщенность порового пространства i-ой
фазой -
; насыщенность порового пространства i-ой
фазой - ![]() .
.
![]() ;
; ![]() .
.
Масса i-ой
фазы в данном объёме ![]() :
:
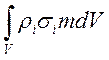 .
.
Скорость изменения массы i-ой
фазы в рассматриваемом объёме ![]() :
:
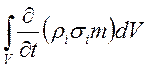
должна быть равна секундному
массовому расходу i-ой фазы через поверхность ![]() :
:
![]() ,
,
т. е.
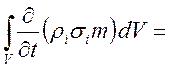
![]() . (11)
. (11)
На основании формулы Остроградского-Гаусса:
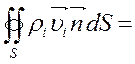
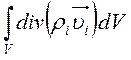 .
(12)
.
(12)
(11) запишем в виде:
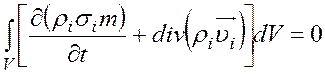 . (13)
. (13)
В силу произвольности объёма ![]() из (13) получим:
из (13) получим:
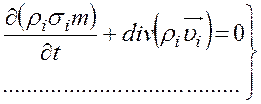 .
(14)
.
(14)
Система (14) – система дифференциальных уравнений неразрывности фаз при фильтрации в однородной пористой среде.
Для двухфазной системы уравнения неразрывности записываются в виде:
для вытесняющей
фазы: ![]()
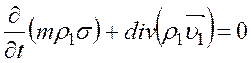 ; (15)
; (15)
для вытесняемой
фазы: 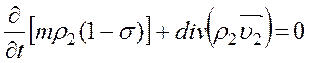 . (16)
. (16)
Если вытесняющая и вытесняемая фазы - слабосжимаемые жидкости (вода-нефть), т.
е. ![]() ;
; ![]() , а
пористую среду также считать несжимаемой (
, а
пористую среду также считать несжимаемой (![]() ), то
уравнения (15) (16) приводятся к виду:
), то
уравнения (15) (16) приводятся к виду:
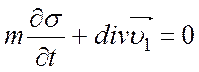 ; (17)
; (17)
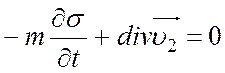 .
(18)
.
(18)
б) Уравнения движения фаз.
Из уравнений неразрывности (14) и закона фильтрации фаз (4) можно получить дифференциальное уравнение движения фаз:
– для многофазной системы:
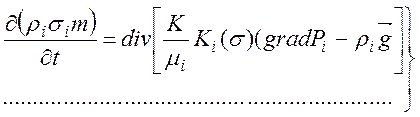 ;
(19)
;
(19)
– для двухфазной системы (если жидкости – несжимаемые; пористая среда – несжимаемая):
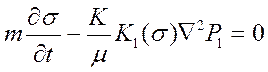 ; (20)
; (20)
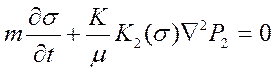 . (21)
. (21)
Наиболее разработана в настоящее время теория одномерного (прямолинейно-параллельного и плоскорадиального) движения двухфазной жидкости в пористой среде.
Рассмотрим прямолинейно-параллельное вытеснение нефти водой вдоль оси Х.
При этом предполагается:
------ жидкости – взаимно нерастворимы и несжимаемы;
------ пористая среда – недеформируема;
------ фазовые переходы отсутствуют;
------ коэффициенты вязкости фаз постоянны;
------ относительные фазовые проницаемости и капиллярное давление
являются известными функциями насыщенности.
 |
![]()

![]()
![]()
![]()
 зона
нефть Х
зона
нефть Х
![]() смеси
смеси
![]()
![]()
![]() вода
вода
![]()
![]()
![]()
![]() g
g![]()
![]()
![]()
Уравнения неразрывности для фаз:
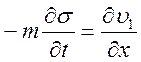 ;
; ![]()
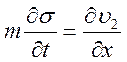 .
(22)
.
(22)
Закон фильтрации (4) сводится к уравнениям:
![]()
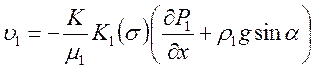 (23)
(23)
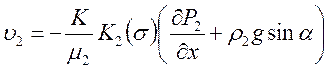
Неизвестные
параметры: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
![]() .
.
Давления ![]() и
и ![]() связаны
соотношением:
связаны
соотношением:
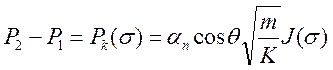 . (24)
. (24)
Система уравнений (22,23,24) может быть сведена к одному уравнению для насыщенности (1953 г., Л. Рапопорт и В. Лис).
Сложив уравнения неразрывности (22) для обеих фаз, получим:
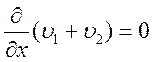 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.