Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 16

Математический смысл метода суперпозиции заключается в том,                   что если имеется несколько фильтрационных потоков с потенциалами:

                           ,

каждый из которых удовлетворяет уравнению Лапласа:

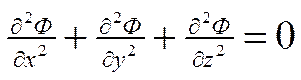                                          ,                                          (6)                                          

то и сумма:  

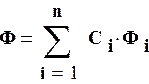                                         (где  С-  произвольные

 постоянные) также удовлетворяет уравнению Лапласа.

           Гидродинамически метод суперпозиции состоит в том,  что изменения потенциала и давления в любой точке пласта,  вызванные работой каждой скважины (добывающей или нагнетательной), алгебраически суммируются в каждой точке пласта. При этом суммарная скорость фильтрации находится как сумма векторов скоростей фильтрации, вызванных работой каждой скважины.

          Пусть на неограниченной плоскости расположено  n источников и стоков:

          Потенциал каждого из них в точке М:

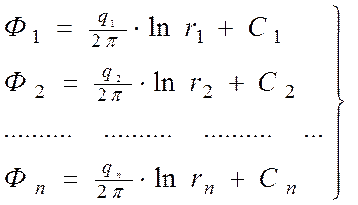                                                                 (7)

 (для стока   q > 0;      для источника   q < 0 ).

Каждая из функций       удовлетворяет уравнению  Лапласа. 

Тогда сумма потенциалов:

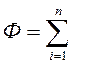
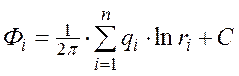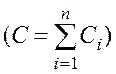                         ,                              (8)

также удовлетворяет уравнению Лапласа,  т.е. определяет суммарный потенциал в точке М.

          Это означает, что фильтрационные потоки от каждого источника или стока накладываются друг на друга (складываются как векторы). 

          Вектор скорости фильтрации    в точке М:

                                     ,                       (9)

   где                               .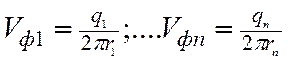

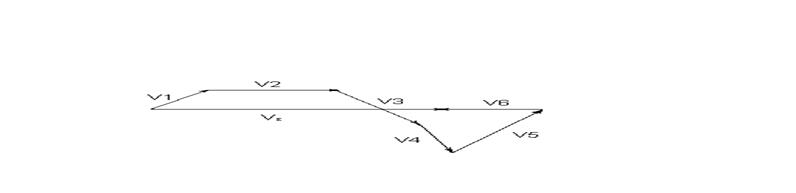
          Метод суперпозиции можно использовать не только в бесконечных пластах, но и в пластах, имеющих контур питания или непроницаемую границу. В этом случае для выполнения граничных условий приходится вводить фиктивные скважины-стоки или скважины-источники за пределами пласта.

           3. Приток жидкости к группе скважин в пласте                             

                           с удаленным  контуром питания.

          Пусть в горизонтальном пласте толщиной  hрасположена группа скважин    А1…Аi…Аn,     работающих с различными забойными потенциалами    Фс1…Фсi…Фсn .  Расстояние между  i  и  j  скважинами - rij.    Радиус скважины ….rC.   Потенциал    Фк на контуре питания считается заданным.   Требуется определить дебит каждой скважины и скорость фильтрации в любой точке пласта.

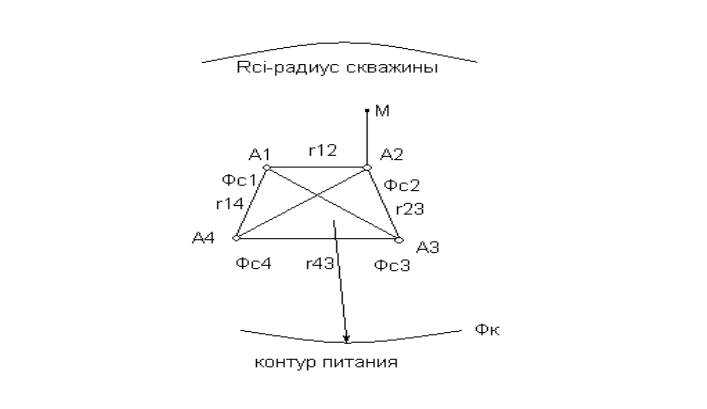
Потенциал в любой точке пласта определяется по формуле (8).

В частности забойные потенциалы на каждой скважине будут равны.

Если  поместим точку  М  на забой скважины   1…i…n, то получим:

     
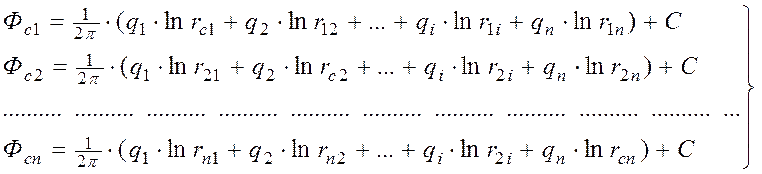
                                                                                                                              (10)

Система (10) состоит из   n уравнений и содержит  n+1 неизвестных

                    (n дебитов  и  постоянную С ).

Дополнительное уравнение получим, определив Фк :

                        .                      (11)

Вычитая  почленно из уравнений системы (10) уравнение (11), исключим C и получим систему из  nуравнений с n неизвестными (q_i).

                .

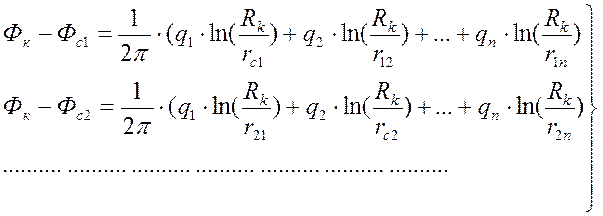(12)                                                                                        

Решив систему (12) можно определить дебиты всех скважин.

    Скорость фильтрации     в любой точке пласта М определяется как векторная сумма скоростей фильтрации, вызванных работой каждой скважины:

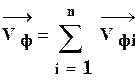                                                                     ,                                 (13)

 где 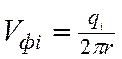                                         .                                               (14)

        направлена по радиусу от точки  М к данной скважине-стоку.

VII.Метод отображения источников и стоков

   1.Приток жидкости к скважине в пласте с прямолинейным
                                      контуром питания.

  Пусть в полубесконечном  пласте с прямолинейным контуром питания работает одна добывающая скважина А с забойным потенциалом Ф_с. Требуется найти дебит скважины q , потенциал Ф и скорость фильтрации в любой точке пласта .