Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 24

Из (31) 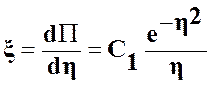                                               .                        (32)

Интегрируем (32) в пределах  :

                                                            .                     (33)

т.к.    ,             то            ,                     (34)

откуда 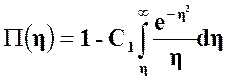                              .                                      (35)

Из (32)                  (36)

Таким образом:                                   ;

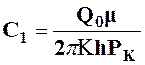
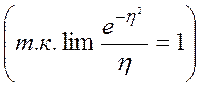т.е. 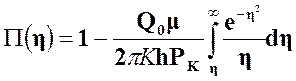                                          .                               (37)

Сделаем подстановку:

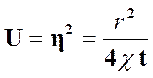                                                         .                                    (38)

Тогда:

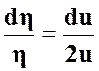
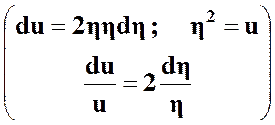                                                          (39)

и перейдем в (37) к размерному давлению: :

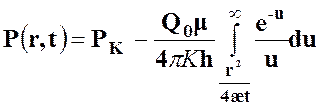                                          .                        (40)

Интеграл 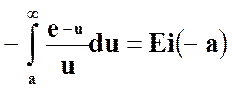              называется интегральной показательной функцией, которая табулирована.

График функции   Е_i(-х)   приведен на рис.1.

         

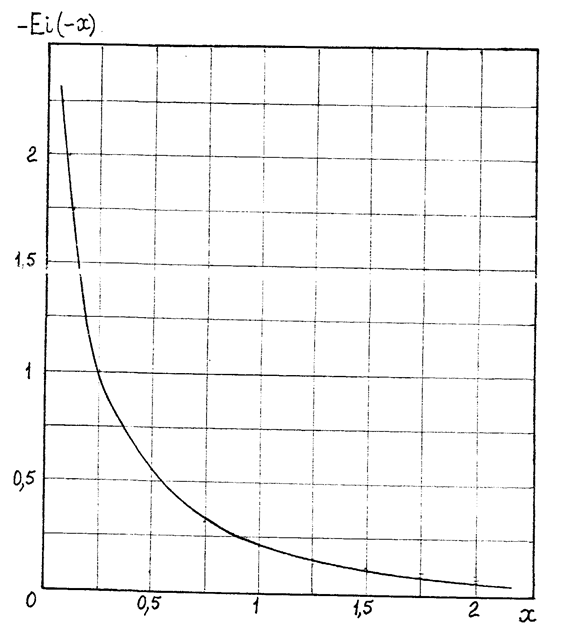
                                                      Рис.1.

                          График интегральной показательной функции.

        Таким образом, давление в любой точке плоскорадиального потока в условиях упругого режима фильтрации определяется по формуле:

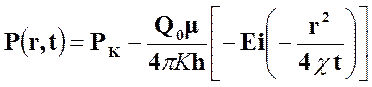            .                         (41)

Формула (41) называется основной формулой упругого режима фильтрации. Она имеет широкое практическое применение, и, в частности, используется при интерпретации результатов исследования скважин.

  Из  выражения (41) расход жидкости через любую цилиндрическую поверхность радиуса r будет равен:

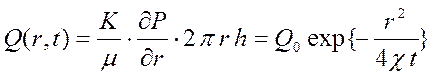                      .                          (42)

 

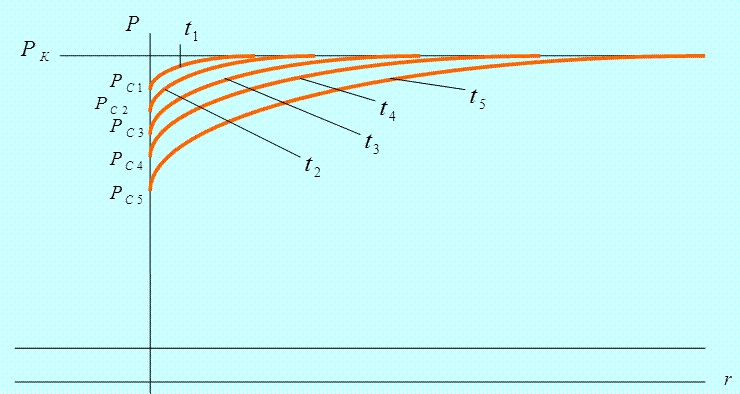
           Рис.2.   Изменение кривых депрессии в призабойной зоне скважины
                          после    пуска  ее в эксплуатацию с постоянным дебитом Q_0..

При малых значениях аргумента 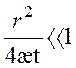           интегральная показательная функция имеет простую асимптотику:

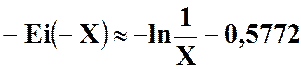                                      .                                            (43)

Следовательно, в этом случае:

                        .                     (44)

     5. Интерференция скважин в условиях упругого режима.

          Для анализа взаимовлияния скважин в условиях упругого режима  применяется метод суперпозиции.

         А.   Если в пласте действует группа скважин, то понижение давления в какой-либо точке пласта    определяется сложением понижений давления, создаваемых в этой точке отдельными скважинами:

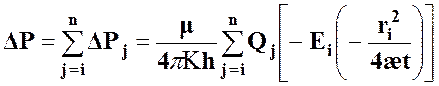                          ,                        (45)                              

       где  n – число скважин;    Q_j – дебит j-ой скважины;

Q_j0, если скважина эксплуатационная;

Q_j0, если скважина нагнетательная.

r_j – расстояние от центра j-ой скважины до рассматриваемой точки.

         Б.   Если скважины начали работать в разное время, то понижение давления в рассматриваемой точке в данный момент времени:

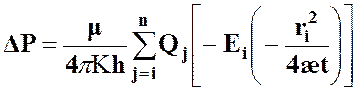                                   ,  (46)

          где t_j – время, прошедшее с начала работы j-ой скважины.

         В.   Если скважина была пущена в эксплуатацию с постоянным дебитом Q   и через промежуток времени  Т  остановлена, то давление в любой точке пласта в момент  t  после остановки можно определить из следующих соображений.

         Предположим, что скважина продолжает работать с тем же дебитом; тогда к моменту t после остановки понижения давления в какой-либо точке пласта, вызванное пуском непрерывно работающей скважины, будет равно:

        .                      (47)

Допустим, что в том же месте, где расположена эксплуатационная скважина, в момент остановки начала работать нагнетательная скважина с тем же дебитом.  К моменту t повышение давления в какой-либо точке пласта, вызванное пуском нагнетательной скважины, равно:

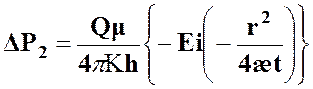              .  (48)

Результирующее понижение давления  будет равно:

        .          (49)

Если аргументы функций малы, то можно использовать приближенную формулу:

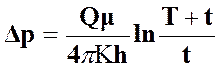                                                     .                                               (50)