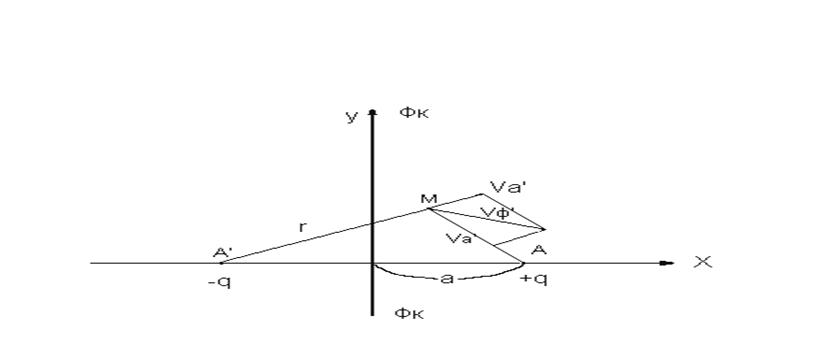
Для решения данной задачи используется так называемый “метод отображения источников и стоков”.
Зеркально отобразим скважину-сток А относительно контура питания скважиной-источником А’ с таким же по величине дебитом. В итоге получаем бесконечный пласт, в котором рассмотрим совместную работу двух скважин: стока А и источника А’.
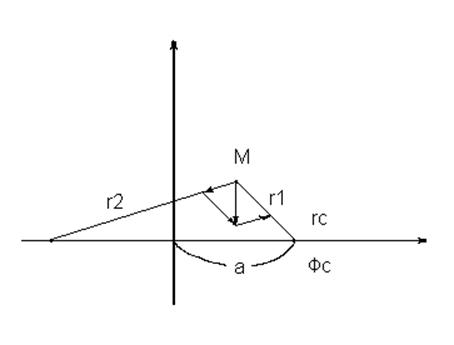
Потенциал в любой точке пласта М:
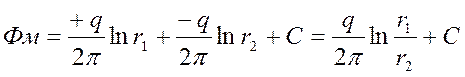 . (1)
. (1)
Если точка М на контуре питания, то ![]() , и потенциал на контуре питания будет
равен:
, и потенциал на контуре питания будет
равен:
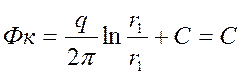 ;
(2)
;
(2)
т.е. потенциал на контуре питания в данном случае остаётся постоянным.
Потенциал на забое скважины А : ![]() ;
; ![]() ;
;
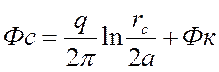 . (3)
. (3)
Из (3) определяем дебит скважины А :
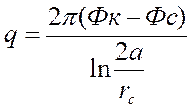 . (4)
. (4)
Если бы контур питания был окружностью радиуса ![]() , то дебит скважины по формуле Дюпюи был бы
равен:
, то дебит скважины по формуле Дюпюи был бы
равен:
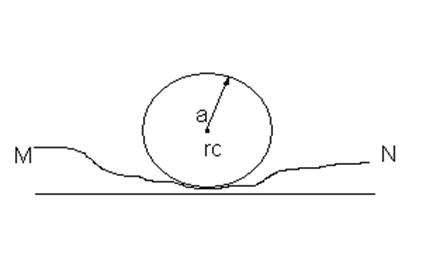
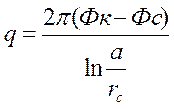 . (5)
. (5)
В реальных условиях форма контура питания MN обычно заключена между окружностью и прямой линией, т.е.:
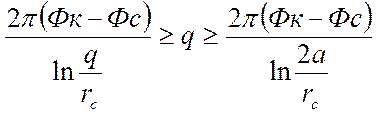 . (6)
. (6)
Потенциал в любой точке М :
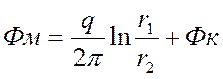 .
(7)
.
(7)
Скорость фильтрации в любой точке М равна векторной сумме скоростей фильтрации , вызванных работой реальной скважины стока А и фиктивной скважины – источника А’.
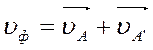 .
. ![]() (
(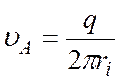 ). (8)
). (8)
Используя 7) и (8) можно построить гидродинамическую сетку
фильтрационного потока:
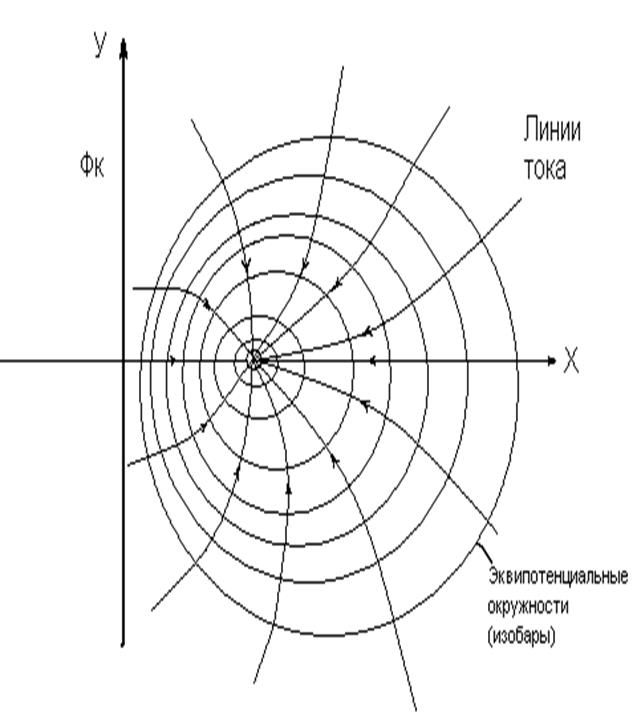
Гидродинамическая сетка фильтрационного потока жидкости к скважине, расположенной вблизи прямолинейного контура питания.
Такая задача может возникнуть при расположении добывающей скважины возле сброса или границы выклинивания продуктивного пласта.
В этом случае реальную скважину-сток зеркально отображают относительно непроницаемой границы фиктивной скважиной-стоком. Решение аналогично предыдущему случаю. В данном случае скорость фильтрации на непроницаемой границе направлена вдоль границы, т.е. граница является линией тока и фильтрация через неё отсутствует.
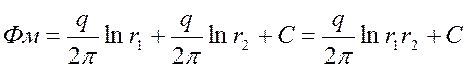 . (9)
. (9)
![]() ;
; ![]() ;
;
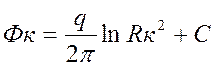 .
(10)
.
(10)
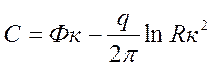 .
(11)
.
(11)
![]() ;
;
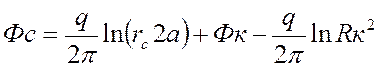 . (12)
. (12)
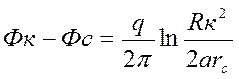 . (13)
. (13)
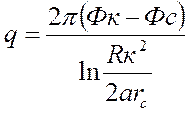 . (14)
. (14)
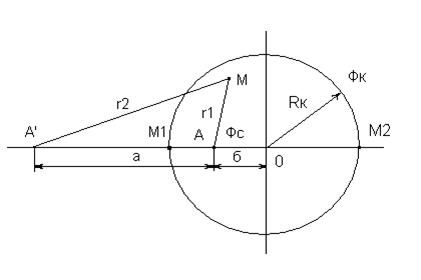
Пусть в плоском пласте постоянной толщины h с круговым контуром питания радиуса Rк, на котором поддерживается постоянный потенциал Фк, эксцентрично расположена скважина-сток А, на которой поддерживается постоянный потенциал Фс. Требуется определить дебит скважины и потенциал в любой точке пласта .
Отобразим скважину-сток А фиктивной
скважиной-источником А’ , расположенной на расстоянии а от скважины А.
Расстояние а определим из условия постоянства потенциала на окружности контура
питания (в точках ![]() и
и ![]() ).
).
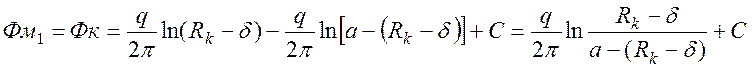 .
.
(15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.