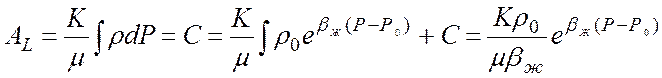Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 20

     .       (14)

          Рассмотрим  плоскорадиальный  приток  сжимаемой  жидкости  к скважине.  Формулу  дебита  скважины  с учетом  сжимаемости  можно получить из формулы Дюпюи,  заменяя объемный расход Q   массовым  Q, а потенциал  Ф  функцией Лейбензона   А.

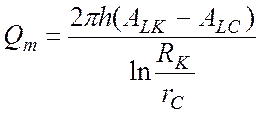                                          ,                                      (15)

где 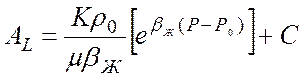                                   .                               (16)

Тогда:

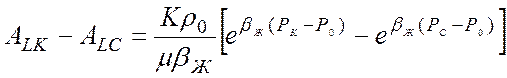                    .                 (17)

           Раскладывая e в ряд  (e^x = 1 + X + 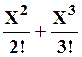+…)   и   ограничиваясь тремя первыми членами разложения    из (17)  получим:

             е- е = β_ж(P_K - P_C)[1+(P_K + P_C -2ρ₀)] ;         (18)

Таким образом:    Q_m = 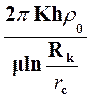[1+ (P_K + P_C -2Р₀)](P_K - P_C).                       (19)

Давления в предыдущих формулах абсолютные. Если положить  P₀ = P_ат  и перейти к избыточным давлениям   P_K  и  P_C,  то :

                               Q_m = 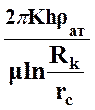[1+(P_K + P_C)](P_K - P_C) .                        (20)

          Разность между объемным дебитом с учетом сжимаемости и дебитом, определенным по формуле Дюпюи,  равна:

                                          ∆Q =  = 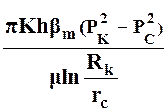.                               (21)

          Распределение давления для упругой жидкости можно получить из распределения давления для несжимаемой жидкости при плоскорадиальной фильтрации:

                                            P = P_K - 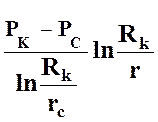.                                         (22)

          Заменим в выражении (22)  P   на    А_L:

                                       А_L = А_LK 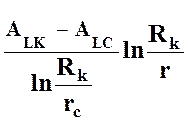.                              (23)

          Используя (14), выражение (23) запишем в виде:

              е = е - 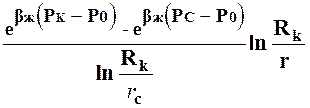.        (24)       

Положив  в (24)  P₀ = P_K    и прологарифмировав это выражение, получим:

                          P = P_K + ln [1-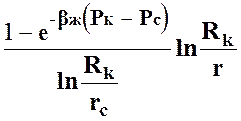].              (25)

 

                   Р           упругая жидкость

 

                Р

 

                                          несжимаемая жидкость

                Р

                      r                                                                                     r

                      Распределение давления в призабойной зоне скважины.

                            3. Прямолинейно-параллельный

                     фильтрационный поток идеального газа.

          Функция Лейбензона для идеального газа  (ρ = ρ_ат ) имеет вид:

                      А _L =  =  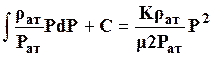+С.                  (26)

          Используем аналогию между фильтрацией  несжимаемой жидкости и фильтрацией газа.

          а) Распределение давления (потенциала) в прямолинейно-параллельном фильтрационном потоке несжимаемой жидкости:

P = P_K - 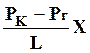.                                    (27)

          При фильтрации газа аналогичное соотношение справедливо для функции Лейбензона:

                                              А = А _K - 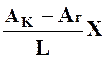         ,                                       (28)

              А_K =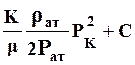;                  А_Г = 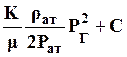.              (29)

          Из (28) с учетом (26) и (29) получим распределение давления при  прямолинейно-параллельной фильтрации  идеального газа:

                                              P= 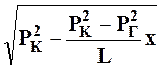         .                                       (30)

          б) Объемный расход несжимаемой жидкости в данном одномерном потоке

Q = 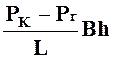.                                     (31)

P=Ф.  

          Массовый расход газа получим, заменив  Pна  А_L:

                                Q_m = 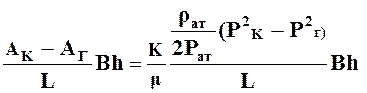.               (32)

          в) вместо скорости фильтрации для несжимаемой жидкости

          υ_ф=  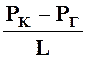   при фильтрации газа аналогично определяется массовая скорость фильтрации:

ρυ_ф= 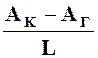 = 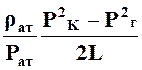.                        (33)         

Откуда скорость фильтрации газа:

                               υ_ф =  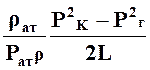=   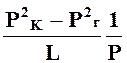       .                   (34)

 4. Плоскорадиальный фильтрационный поток

                              идеального газа по закону Дарси.

          Плоскорадиальный фильтрационный поток имеет место в круговом пласте радиусом R_K, в центре которого имеется совершенная скважина радиусом   r_C.