Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 35

           В трещиновато-пористом пласте дебит скважины складывается из дебита жидкости, притекающей из трещин, и из дебита жидкости, поступающей из пористых блоков.

           Суммарный дебит добывающей скважины в круговом трещиновато-пористом пласте:

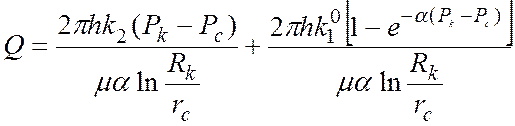                      .              (31)

Первое слагаемое значительно меньше второго и его без существенной погрешности можно отбросить.

XIV. Фильтрация неньютоновских жидкостей

Нефти ряда месторождений (Азербайджана, Башкирии, Татарии, Казахстана – Мангышлак и др.) обладают ярко выраженными неньютоновскими свойствами, что связано в основном с повышенным содержанием в них высокомолекулярных компонентов: смол, асфальтенов, парафина. Фильтрация неньютоновских жидкостей обладает рядом особенностей и не подчиняется линейному закону фильтрации Дарси.

         1. Законы фильтрации неньютоновских жидкостей.

Закон фильтрации неньютоновских жидкостей зависит от типа ее реологической модели.

Наиболее широкий класс нефтей с ярко выраженными неньтоновскими свойствами относится к типу вязкопластичных жидкостей, реологическая модель которых – модель Бингама:

                                   

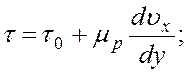
                                                                                                                (1)

                                   ;                

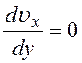где    - начальное напряжение сдвига.

При    - вязкопластичные жидкости ведут себя как твердое тело;

при     - текут как обычные вязкие жидкости.

Рассмотрим стационарное течение вязкопластичной жидкости в одной поре – цилиндрической капиллярной трубке постоянного радиуса.

Максимальное касательное напряжение – на стенках капилляра и убывает при приближении к оси.

На некотором расстоянии  от оси    , т.е. при        .

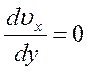Из баланса сил для цилиндрического объема длиной l и радиусом :

                        ,                                          (2)

получим: 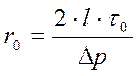                               .                                                  (3)

Очевидно, когда 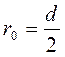   во всем сечении капилляра   , что отвечает случаю полного прекращения движения в данной поре. Из (3) можно определить максимальный перепад давления для этого случая:

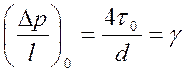                                                       .                                     (4)

 Величина    определяет тот градиент давления 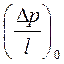 , по достижении которого начнется движение жидкости в поре. При меньших значениях градиента давления движение отсутствует. Величина    называется предельным (начальным) градиентом.

 Величина γ зависит от предельного напряжения сдвига τ₀ и среднего диаметра пор.

        Так как характерный размер пор пористой среды

,

где k – проницаемость,

то 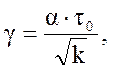                                                      .                                            (5)

где α – безразмерная константа.

           Закон фильтрации вязкопластичной жидкости можно сформулировать в виде:

                                   , 

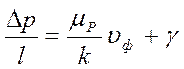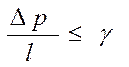                                        ,                                                 (6)

или в векторной дифференциальной форме:

                           ,  

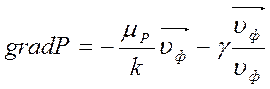                                             ,                                         (7)

В  соответствии с (6) или (7) скорость фильтрации отлична от нуля только в тех областях, где .

В пористой среде, состоящей из множества микрокапилляров различных диаметров, при снижении перепада давления начинается постепенное “закупоривание” капилляров. Вначале движения прекращается в наиболее мелких порах, а по мере снижения давления происходит закупоривание все больших и больших капилляров. В пластах со слоистой неоднородностью наблюдается закупоривание целых пропластков (прекращение движения в них нефти) по мере снижения пластового давления.

При фильтрации псевдопластичных жидкостей, реологическое уравнение которых ------ модель Оствальда – де Вейля:

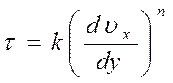                                ,                                         (8)

используют степенной закон фильтрации: