Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 5

          При весьма малых скоростях жидкости сила вязкого трения мала по сравнению с силами межфазового взаимодействия  жидкости с твердой поверхностью. При увеличении скорости жидкости уменьшается вклад межфазового взаимодействия в гидравлическое сопротивление пористой среды, но возрастает вклад обычного гидродинамического вязкого трения.          Для фильтрации при малых скоростях предложена следующая упрощенная зависимость:

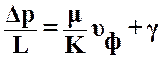                                                       .                                      (22)

 ---начальный градиент давления, необходимый для начала фильтрации.

II. Дифференциальные уравнения фильтрации

 флюидов в нефтегазоносных пластах

          Основной кинематической характеристикой движения флюида в пласте является скорость фильтрации , которая может быть различной в разных точках пласта и переменной во времени – т.е. образует физическое поле скоростей фильтрации.

           Поле  может быть стационарным и нестационарным.

          Скорость фильтрации  существенно зависит от распределения давлений в пласте, т.е. от поля давлений ; распределения температур в пласте ; от пористости пласта ; его проницаемости .

          Существенны также плотность флюида  и его вязкость .

          Процесс фильтрации может быть изотермическим, если  и одинакова во всем пласте; и неизотермическим (например, при закачке в пласт горячей воды, пара).

          Система дифференциальных уравнений фильтрации включает в себя: уравнение неразрывности; дифференциальное уравнение движения; уравнения состояния флюида и пористой среды.

                                 1. Уравнение неразрывности.

Уравнение неразрывности является частным случаем закона сохранения массы для движущегося в пористой среде флюида.

Рассмотрим конечный неизменный объем пористой среды V, ограниченный поверхностью S.

                                                                       

                                                             V                                     

                                                 S                           

 

                                                                               

В общем случае считаем флюид сжимаемым, т.е. , а пористую среду упруго-деформируемой, т.е. .

          Масса флюида в данном объеме пористой среды V:

                                                         .

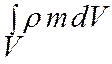          Изменение массы флюида в данном объеме пористой среды связано с изменением плотности  или пористости  и может происходить только за счет разности втекания и вытекания флюида через поверхность S.

          Скорость изменения массы флюида в объеме V:

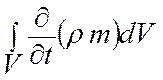
должна быть равна секундному массовому расходу флюида через поверхность S:

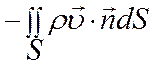
( - скорость фильтрации)

(входящий поток отрицателен, т.к. противоположен по направлению нормальному вектору поверхности  ; выходящий – положителен; т.о. при положительной скорости изменения массы флюида в объеме V данный интеграл необходимо брать со знаком «минус»).

          Итак:

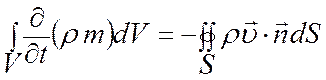                                        .                           (1)

На основании формулы Остроградского-Гаусса:

                                                                                                                                                             .                                                       

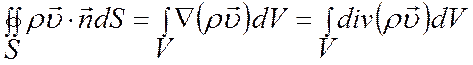                                                                                                                           (2)

 .

Из (1) и (2)

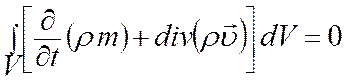                                           .                     (3)

Т.к. объем V выбран произвольно, то

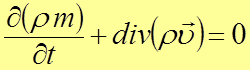                                                 .                              (4)

          Уравнение (4) – дифференциальное уравнение неразрывности флюида в пористой среде в самом общем случае движения (нестационарное движение сжимаемого и несжимаемого флюида в упруго-деформируемой пористой среде).

          Для недеформируемой пористой среды:  m=const, из (4) получаем: