№ кривой соответствует значению 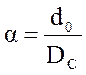 :
:
№ 1 – α = 0.03;
№ 2 – α = 0.04;
№ 3 – α = 0.05;
№ 4 – α = 0.06;
№ 5 – α = 0.07;
№ 6 – α = 0.08;
№ 7 – α = 0.09.
Для хорошо перфорированного забоя скважины С2 << С1.
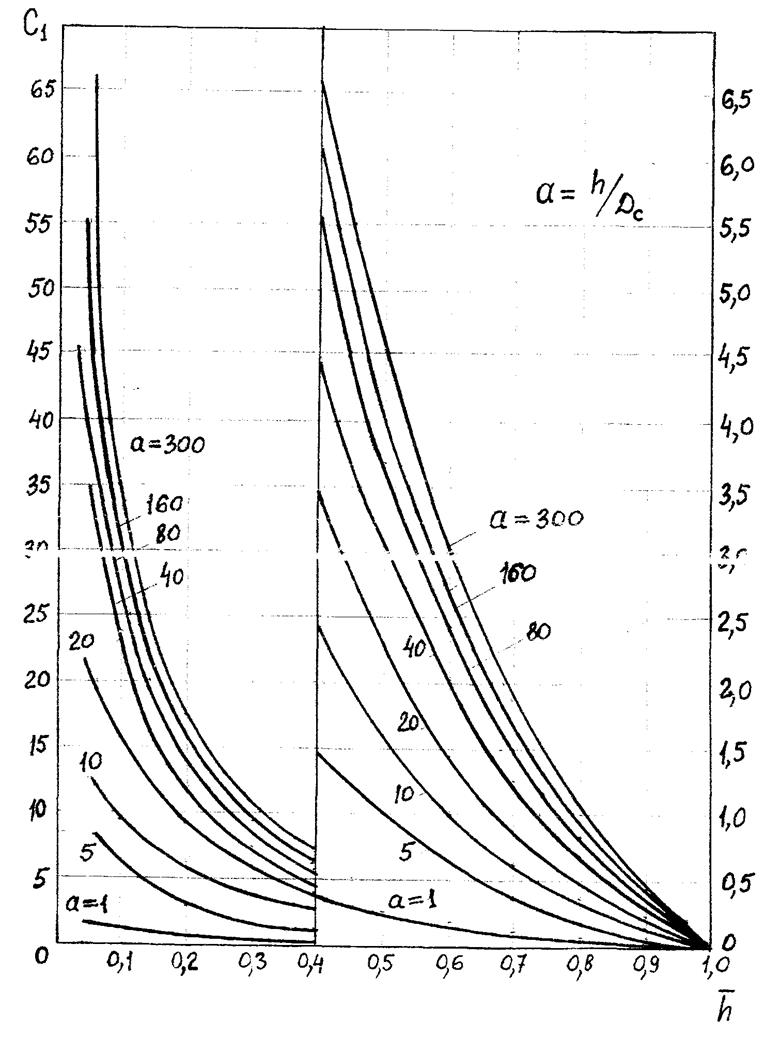
Рисунок 1.

Рисунок 2.
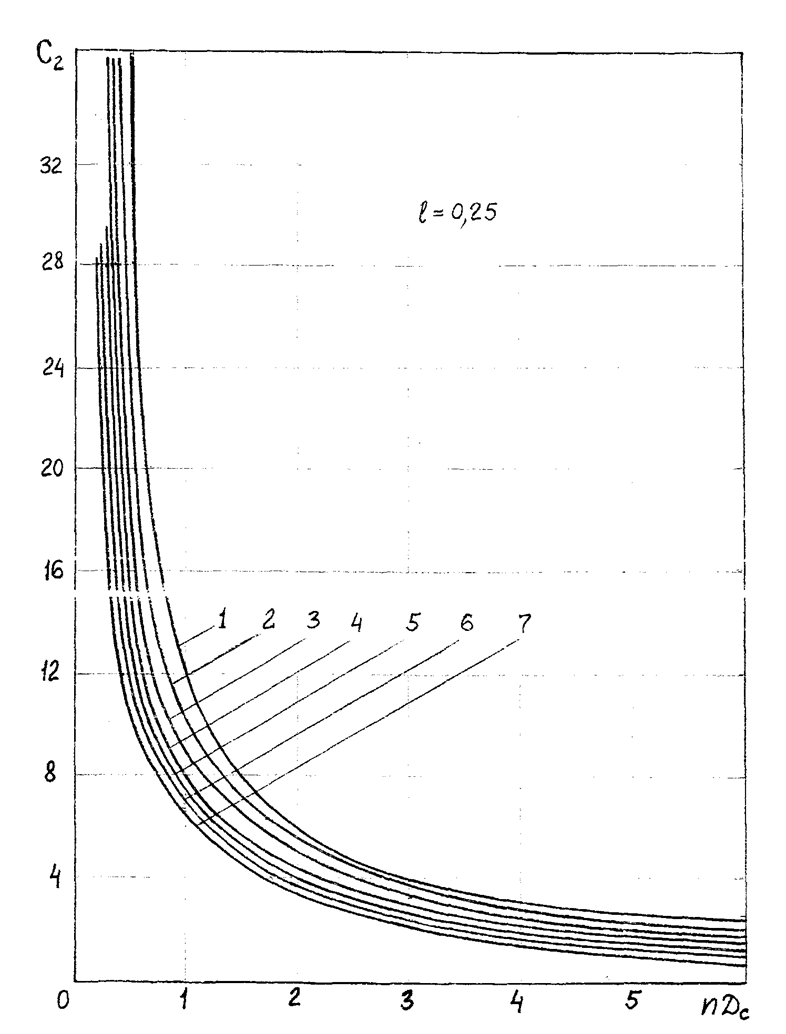
Рисунок 3.
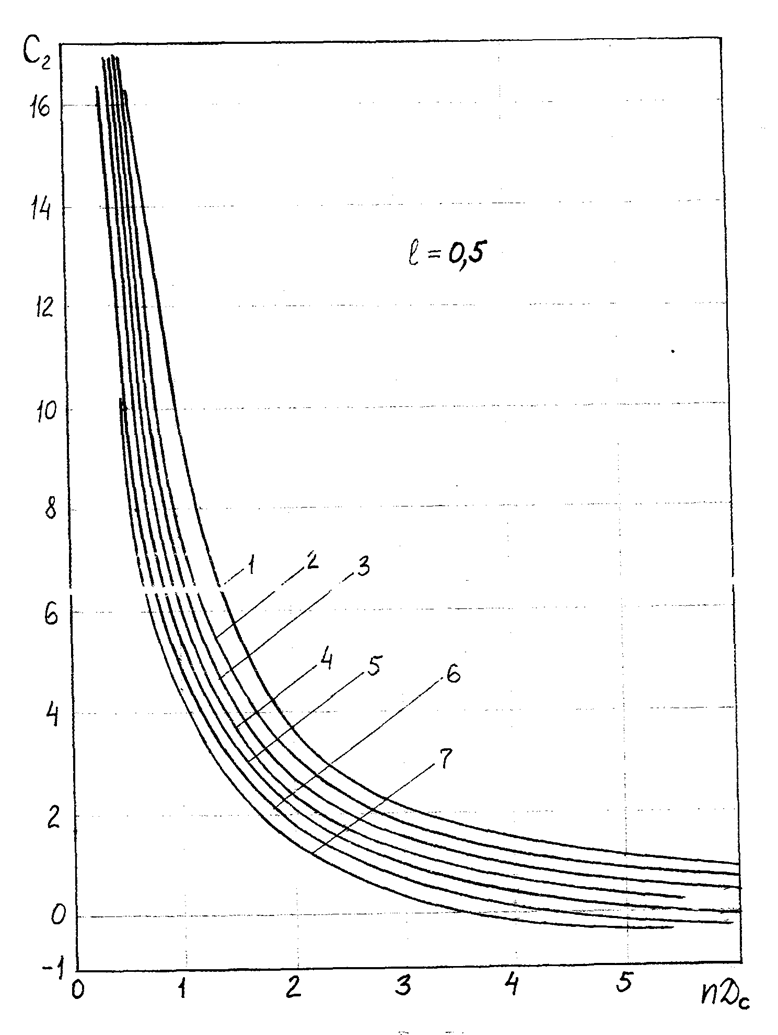
Рисунок 4.
Гидродинамическое несовершенство скважины удобно учитывать при помощи коэффициента совершенства скважины δ, представляющего собой отношение дебита несовершенной скважины Q (5) к дебиту совершенной скважины (формула Дюпюи) в тех же условиях:
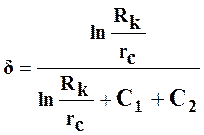 .
(8)
.
(8)
Общее дифференциальное уравнение фильтрации флюида в пористой среде по закону Дарси:
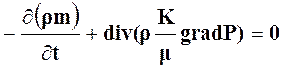 (1)
(1)
или 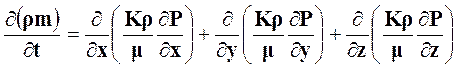 , (2)
, (2)
где в общем случае: ρ(Р); μ(Р); К(Р); m(Р). Р – полное давление.
Введем функцию АL, дифференциал которой:
![]() А
А![]() =
=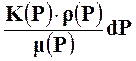 ; (3)
; (3)
т.е. А![]() =
=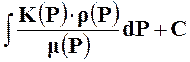 . (4)
. (4)
Функция АL называется функцией Л.С.Лейбензона. АL(P); P(x, y, z, t).
Полный дифференциал функции Лейбензона:
![]() =
(5) ==
=
(5) ==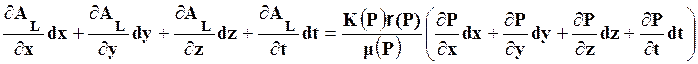 .
.
из (5) 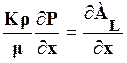 ;
; 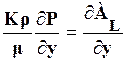 ;
; 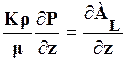 . (6)
. (6)
Т.о. уравнение 2 можно представить в виде:
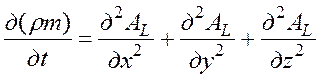 . (7)
. (7)
или 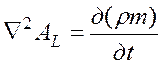 . (8)
. (8)
Дифференциальное уравнение (7) или (8) справедливо для движения (в общем случае – неустановившегося) однородного сжимаемого (упругого) флюида в однородной пористой (в общем случае – деформируемой) среде по закону Дарси.
В случае установившейся фильтрации уравнения (7) и (8) приводятся к виду:
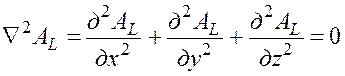 .
(9)
.
(9)
Из
(9) следует, что при установившейся фильтрации упругого флюида функция А![]() удовлетворяет
уравнению Лапласа.
удовлетворяет
уравнению Лапласа.
Введение функции Лейбензона позволяет установить аналогию между установившейся фильтрацией сжимаемого флюида и несжимаемой жидкости, т.е. использовать хорошо известные закономерности фильтрации несжимаемой жидкости.
Для несжимаемой однородной изотопной пористой среды K = const.
Кроме того, будем считать μ= const, а ρ = ρ(P).
Тогда функция Лейбензона записывается в виде:
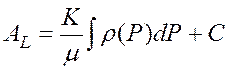 ;
; 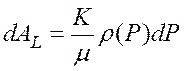 .
(10)
.
(10)
……………………………………………………………………………………
Рассмотрим фильтрацию флюида вдоль некоторой трубки тока.
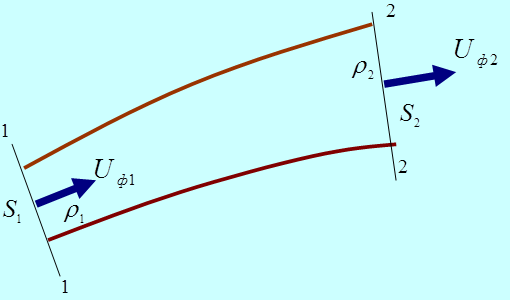
Для сжимаемого флюида массовый расход вдоль трубки тока величина постоянная:
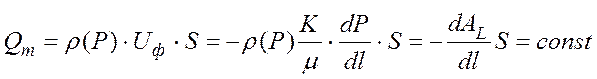 . (11)
. (11)
Для несжимаемой жидкости:
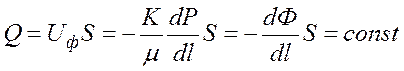 . (12)
. (12)
Из аналогии уравнений Лапласа для фильтрации несжимаемой
жидкости и сжимаемого флюида (9) можно сделать вывод, что все формулы,
полученные для установившейся фильтрации несжимаемой жидкости, можно
использовать и для фильтрации сжимаемого флюида, если в них заменить
потенциал Ф =![]() на функцию Лейбензона A
на функцию Лейбензона A![]() ;
;
вместо объемного расхода Q = υ![]() S использовать
массовый расход Q
S использовать
массовый расход Q![]() =
ρυ
=
ρυ![]() S , а
вместо скорости фильтрации υ
S , а
вместо скорости фильтрации υ![]() использовать массовую скорость ρυ
использовать массовую скорость ρυ![]() .
.
При установившейся фильтрации упругой жидкости, плотность которой:
![]() , (13)
, (13)
функция Лейбензона записывается в виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.