Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 4

При движении жидкости и газа по каналам пористого слоя турбулентность в них развивается значительно раньше, чем при течении по трубам.

Режим течения флюида в пористой среде можно определить с помощью фильтрационного критерия Рейнольдса:

Re=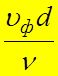 ,                                                   (12)

где d– некоторый характерный линейный размер пористой среды (размер каналов, пор или частиц в зависимости от используемой модели пористой среды);     - кинематический коэффициент вязкости флюида.

          Н.Н. Павловский (1920 годы), основываясь на модели идеального пористого слоя, предложил следующее выражение фильтрационного числа Рейнольдса:

Re = 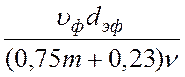.                                  (13)

          Установлено (Н.Н.Павловский), что при  Re < 7,5…9   сохраняется ламинарный режим фильтрации и действует линейный закон фильтрации Дарси.  

           При   Re > 7,5…9  ламинарный режим фильтрации нарушается ----фильтрация становится неламинарной.

          В.Н.Щелкачев предложил  в качестве линейного параметра пор использовать следующую величину:

d = 10m;                                       (14)

                                                                                                                                                                                      

т.е. число  Рейнольдса  по  Щелкачеву:

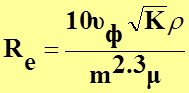                                            .                                              (15)

          Критические значения числа Рейнольдса по Щелкачеву находятся в пределах   Re= 1…12.

          М.Д. Миллионщиков предложил следующее выражение для числа Рейнольдса:

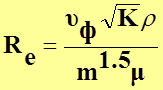                                                 .                                             (16)

По Миллионщикову:Re = 0,022 … 0,29.                                    

          Для неламинарного режима фильтрации предложен нелинейный закон фильтрации  Форхгеймера:

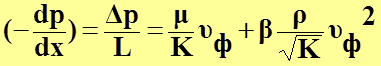  ,                       (17)

где β – дополнительная константа пористой среды, определяемая экспериментально, либо приближенно по формуле А.И. Ширковского:

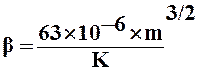.                                  (18)

В выражении (17):

         I слагаемое 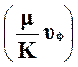 учитывает потери давления вследствие вязкого трения жидкости в поровых каналах;

        II слагаемое 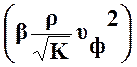 учитывает инерционную составляющую сопротивления движению жидкости, связанную с турбулизацией течения.

          При малых скоростях фильтрации (точнее при малых числах Рейнольдса):

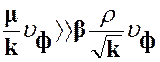               ²          и закон Форхгеймера переходит в закон Дарси:

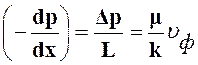                                            .                                              (19)

          При увеличении числа Рейнольдса  значение II слагаемого возрастает.

          При больших скоростях фильтрации (т.е. числах Рейнольдса)

 IIслаг.Iслаг.----- наступает турбулентный режим фильтрации с квадратичным законом сопротивления (Краснопольский А.А.):

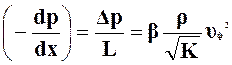.                                         (20)

Квадратичный закон фильтрации наблюдается лишь в средах, состоящих из крупных частиц.

          Для описания закономерностей неламинарной фильтрации используются также нелинейные законы в виде одночленной степенной функции:

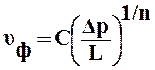,                                           (21)

где С и n – опытные параметры:   1  ≤ n ≤2 ;

                                                                                                                        

          4. Особенности фильтрации при малых скоростях.

          При очень малых скоростях флюида в пористой среде обнаруживается существенное отклонение от закона Дарси, проявляющееся в более быстром увеличении скорости  фильтрации  с ростом градиента давления     P/L.

          Это явление особенно заметно при фильтрации жидкостей (воды, нефти) в тонкозернистых  (глинистых) породах.

          Объясняется это явление тем, что жидкость (в том числе, нефть) определенным образом физико-химически взаимодействует с поверхностью твердого тела (этим же объясняется модель «прилипания» жидкости). Пористые тела имеют весьма развитую поверхность. В результате тончайшие слои жидкости около твердой поверхности образуют загустевшие студнеобразные структуры, частично или полностью перекрывающие поры. Чтобы началось движение, нужно разрушить эту структуру, приложив некоторый перепад давления.