Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 3

          Основной характеристикой фильтрационного движения флюида в пористой среде является  скорость фильтрации  _. – фиктивная скорость, равная отношению действительного расхода флюида через выделенную площадку  к ее площади:

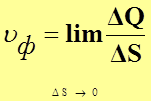                                                        ,                                          (4)

      ∆S  –  полная площадь, а не ее часть, занятая порами  ∆S_n.

          Действительная скорость движения флюида через площадку ∆S:

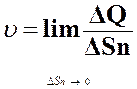
.                                               (5)                                                                              

                                                          

Так как    ∆S_n = m ∆S,  то фиктивная скорость фильтрации    и действительная скорость движения флюида   связаны соотношением:

                                            .             (   <   ).                     (6)

    2. Закон фильтрации Дарси.

Реальная пористая среда оказывает сопротивление фильтрационному потоку флюида. Т.е. для поддержания фильтрационного течения флюида в пористом теле необходимо к нему приложить определенную разность давлений (напоров):    ΔР =  Р₁ -  Р₂      ( ΔН = Н₁ – Н₂).

Р₁ > Р₂

H ₁  > H ₂

L

                                                                              V_ф; Q

              

                                                                          x

                S – площадь поперечного сечения слоя.

          Основное соотношение теории фильтрации – закон фильтрации – устанавливает связь между скоростью фильтрации (расходом) и распределением давлений (напоров), которое вызывает фильтрационное течение.

          Простейшим законом фильтрации является линейный закон фильтрации Дарси (1856г.):

Q = K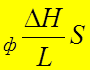 .                                              (7)

K_ф – коэффициент фильтрации; зависит как от структуры пористой среды, так и от свойств флюида ( вязкости);  его размерность: м/с.

          Позднее закон фильтрации был сформулирован в виде:

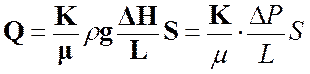,                       (8)

где  – динамический коэффициент вязкости флюида,

 К – коэффициент проницаемости пористой среды (не зависит от свойств флюида и является фильтрационной характеристикой только пористой среды) .  [K] = м.

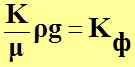 .                                              (9)

Выражение (8) можно записать в виде:

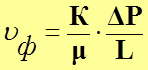                                                                                                                                                                              (10)

или в дифференциальной форме:

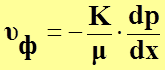,                                                                                                                          (11) где   х  – продольная ось фильтрации.

Знак «минус» появился в выражении (11) вследствие того, что давление вдоль оси х (т.е. направления фильтрационного движения флюида) уменьшается.

          Коэффициенты  проницаемости:  К (м²):

                       крупнозернистый песчаник: 10^-12 ÷ 10^-13 ;

                       плотные песчаники: 10^-14 ÷ 10^-15  .

          Проницаемость нефтяных и газовых пластов измеряется единицами, называемыми Дарси (Д).

          За единицу проницаемости 1Д принимают проницаемость такой пористой среды, при фильтрации через образец которой площадью 1 см² длиной 1 см при перепаде давления в 1 атм (98000 Па) расход жидкости вязкостью  1 сП (вода 20⁰С)   составляет 1 см³/с.

1Д = 1,02 10^-12 м².

Средние скорости фильтрации в нефтяных пластах: = 10^-4 ÷ 10^-5 м/с.

          Течение флюида через пористый слой может быть ламинарным и неламинарным (турбулентным).

          Линейный закон фильтрации Дарси удовлетворительно описывает фильтрационные течения нефти, газа, грунтовых вод и т.д. при ламинарном режиме фильтрации, но не слишком малых скоростях фильтрации.

          При неламинарной фильтрации, а также при очень малых скоростях фильтрации обнаруживаются существенные отклонения реальных фильтрационных течений от линейного закона Дарси.

3. Закономерности неламинарной фильтрации.