![]() ,
(5)
,
(5)
где: ![]() -
параметр трещиноватой среды, зависящий от упругих свойств и геометрии трещин.
-
параметр трещиноватой среды, зависящий от упругих свойств и геометрии трещин.
Из выражений (4) и (5) зависимость коэффициента проницаемости трещиноватой породы от давления будет следующей:
![]() . (6)
. (6)
Для пористых сред аналогическая зависимость:
![]() . (7)
. (7)
При рассмотрении
фильтрации в трещиновато-пористом пласте обычно считают, что коэффициент
проницаемости трещин К![]() существенно зависит от давления,
а коэффициент проницаемости пористых блоков К
существенно зависит от давления,
а коэффициент проницаемости пористых блоков К![]() принимается
постоянным (т.е. К
принимается
постоянным (т.е. К![]()
![]() f(р))
.
f(р))
.
Соотношения для установивщихся фильтрационных потоков в трещиновато-пористой среде получаются суммированием потоков в трещинах и пористых блоках.
Система трещин и система пор (трещиновато-пористой среды) представляют собой две среды с разными масштабами:
средний размер пор: 1- 10 (до 100) мкм;
протяженность трещин от нескольких сантиметров до десятков метров.
Следует иметь в виду следующие соотношения:
m2>>m1.
К2<<K1
(2-пористые блоки; 1- трещины);
т.е. жидкость в основном содержаться в пористых блоках, откуда фильтруясь из них в трещины, движется в скважины в основном по трещинам.
Р2>P1; Vф2<<Vф1.
Рассмотрим конечный
объём трещиновато-пористой среды V, ограниченной поверхностью S. Будем считать
что в каждой точке имеются два давления: P![]() – в системе трещин, P
– в системе трещин, P![]() – в пористых блоках; и две скорости фильтрации:
– в пористых блоках; и две скорости фильтрации: ![]() - в трещинах,
- в трещинах, ![]() - в
пористых блоках.
- в
пористых блоках.
Переток жидкости из пористого блока в систему трещин:
![]() q=
q=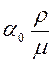 (P
(P![]() -P
-P![]() )
. (8)
)
. (8)
Масса жидкости, содержащаяся в системе трещин объёма V:
![]() .
.
Скорость изменения массы жидкости в трещинах
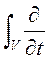 (
(![]()
![]() )dV
)dV
равна массовому потоку жидкости, проходящему через боковую поверхность S в систему трещин или из неё:
-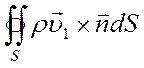
плюс переток жидкости из пористого блока в систему трещин
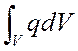
т.е.
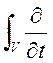 (
(![]()
![]() ) dV= -
) dV= -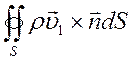 +
+ ![]() . (9)
. (9)
Т.к. 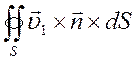 =
=![]()
![]() dV
, то выражение (9) приведём к виду:
dV
, то выражение (9) приведём к виду:
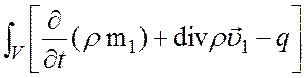 dV=0 (10)
dV=0 (10)
или
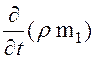 = -
= -![]() .
(11)
.
(11)
(11) – дифференциальное уравнение неразрывности для потока жидкости в системе трещин в трещиновато-пористой среде.
Масса жидкости, содержащаяся в пористых блоках в обьеме V:
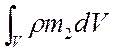 .
.
Скорость изменения массы жидкости в пористых блоках равна массовому потоку жидкости, проходящему через боковую поверхность S в пористые блоки или из них, минус переток жидкости из пористых блоков в систему трещин:
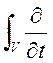 (
(![]()
![]() ) dV=-
) dV=-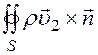 dS-
dS-![]() (12)
(12)
Выражение (12) можно привести к виду:
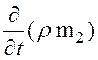 = -
= -![]() .
(13)
.
(13)
(13) – дифференциальное уравнение неразрывности для потока жидкости в пористых блоках в трещиновато-пористой среде.
Для чисто трещиноватого пласта q=0; остаётся только уравнение:
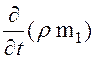 = -
= -![]() .
(14)
.
(14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.