из (10) получим:
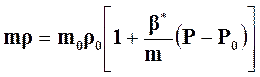 . (11)
. (11)
(11) дифференцируем по t:
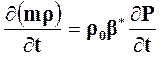 . (12)
. (12)
Функция Лейбензона для упругой жидкости (при умеренных давлениях)
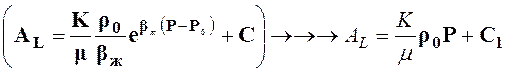 . (13)
. (13)
Дифференцируя (13) дважды по координатам и складывая, получим:
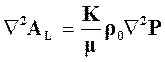 .
(14)
.
(14)
Подставляя (12) и (14) в (7), получим:
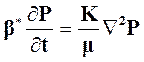 . (15)
. (15)
Обозначим: 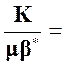 χ. (16)
χ. (16)
Тогда (15) записывается в виде:
![]() = χ
= χ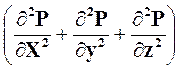 (17)
(17)
или
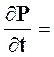 χ
χ ![]() . (18)
. (18)
Уравнение (17) является основным дифференциальным уравнением упругого режима фильтрации. По предложению В.Н.Щелкачева оно названо уравнением пьезопроводности и относится к уравнениям Фурье (уравнениям теплопроводности).
Коэффициент χ, характеризующий скорость перераспределения пластового давления при неустановившейся фильтрации упругой жидкости в упругой пористой среде, называется коэффициентом пьезопроводности пласта (по аналогии с коэффициентом температуропроводности в уравнении теплопроводности).
χ = 0,1![]() 5
5![]() м
м![]() /с.
/с.
Пусть в неограниченном горизонтальном пласте постоянной толщины h имеется добывающая скважина нулевого радиуса (точечный сток).
В
момент времени t![]() во
всем пласте давление Р (r,0) = Рк = const.
во
всем пласте давление Р (r,0) = Рк = const.
В момент t = 0 скважина пущена в эксплуатацию c постоянным дебитом Q0.
В пласте возникает неустановившийся плоскорадиальный поток упругой жидкости. Необходимо определить распределение давления в пласте в любой момент времени: Р (r, t).
Запишем основное уравнение упругого режима фильтрации
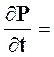 χ
χ![]() (19)
(19)
в цилиндрической системе координат:
![]() χ
χ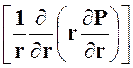 (20)
(20)
или:
![]() = χ
= χ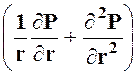 . (21)
. (21)
Начальные и граничные условия:
![]()
![]() ;
; ![]()
![]() υ
υ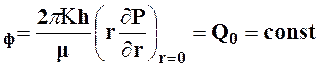 (22)
(22)
t>0
Последнее условие запишем в виде:
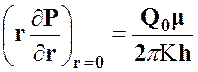 . (23)
. (23)
Для того чтобы проинтегрировать уравнение (3) необходимо перейти к безразмерным переменным:
безразмерное
давление: 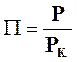 ;
(24)
;
(24)
размерные аргументы r и t можно
объединить в один
безразмерный комплекс: 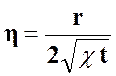 . (25)
. (25)
Тогда ![]()
![]() Очевидно:
Очевидно:
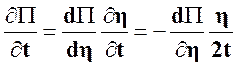
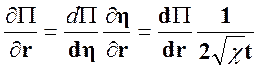 ;
; 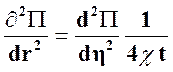 .
(26)
.
(26)
Подставляя (26) в (21) получим обыкновенное дифференциальное уравнение:
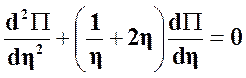 . (27)
. (27)
Граничные условия: при ![]() П
= 1.
П
= 1.
Кроме того (23) запишем в виде:
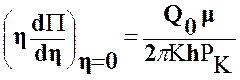 . (28)
. (28)
(Действительно: ![]()
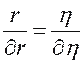 ).
).
Заменим: 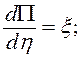 (27) запишем в виде:
(27) запишем в виде: 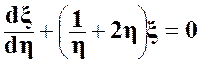 . (29)
. (29)
или:
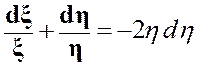 . (30)
. (30)
Интегрируем (30):
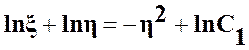 . (31)
. (31)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.