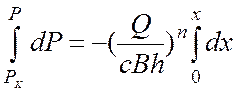 . (6)
. (6)
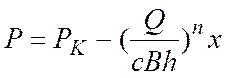 . (7)
. (7)
Подставив в (7) Q из (5) получим:
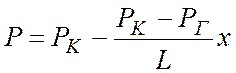 . (8)
. (8)
Таким образом распределение давления при нелинейном законе фильтрации линейно и в точности совпадает с распределением давления в аналогичном потоке при фильтрации по линейному закону Дарси.
Рассмотрим плоскорадиальный фильтрационный поток несжимаемой жидкости, фильтрация которого подчиняется квадратичному закону Краснопольского:
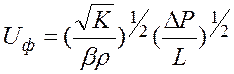 .
(9)
.
(9)
Обозначим 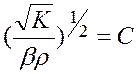 и запишем (9) в дифференциальной
форме:
и запишем (9) в дифференциальной
форме:
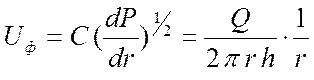 . (10)
. (10)
Из (10) имеем:
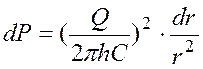 . (11)
. (11)
Интегрируем (11): 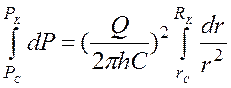 ; (12)
; (12)
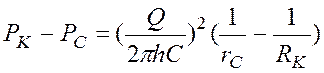 , (13)
, (13)
Откуда:
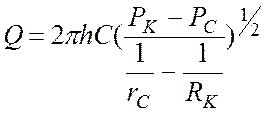 . (14)
. (14)
Так
как ![]() <<
<<![]() , то (14) можно записать в виде:
, то (14) можно записать в виде:
![]() . (15)
. (15)
Проинтегрируем (11) следующим образом:
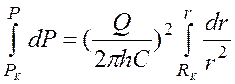 ,
(16)
,
(16)
и используя (14), получим распределение давления в пласте:
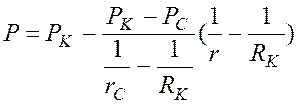 . (17)
. (17)
Таким образом, в данном случае распределение давления имеет тот же вид, что и для линейного закона Дарси, но для радиально-сферического фильтрационного потока.
При пуске, остановке или изменении режима работы одной скважины (или группы скважин) изменяются дебиты и забойные давления других скважин, эксплуатирующих тот же пласт. Суммарная добыча нефти из месторождения по мере ввода в эксплуатацию новых скважин растет медленнее, чем число скважин.
Точечным стоком называется точка, поглощающая жидкость. На плоскости точечный сток можно рассматривать как модель гидродинамически совершенной скважины бесконечно-малого диаметра в пласте единичной толщины.
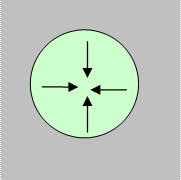 Точечный источник --- это точка, выделяющая жидкость
Точечный источник --- это точка, выделяющая жидкость
(модель нагнетательной скважины).
.
Определим потенциал точечного стока (источника).
На плоскости точечный сток является моделью
добывающей скважины и течение вокруг него
плоскорадиальное.
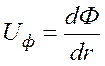 ----- обобщенный
закон фильтрации Дарси; (1)
----- обобщенный
закон фильтрации Дарси; (1)
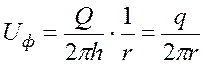 ,
(2)
,
(2)
где 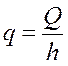 --- дебит
скважины- стока, приходящийся на единицу толщины пласта.
--- дебит
скважины- стока, приходящийся на единицу толщины пласта.
Из (1) и (2) получим:
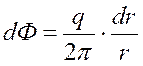 . (3)
. (3)
Интегрируем (3):
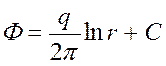 ,
(4)
,
(4)
где С – постоянная интегрирования.
Для точечного
источника:
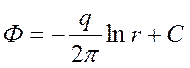 . (5)
. (5)
Понятия источников и стоков широко используются для решения многих
важных задач подземной гидромеханики.
Метод суперпозиции (метод наложения) основан на свойствах уравнения Лапласа, которое описывает распределение потенциала (т.е. давления) в фильтрующихся потоках флюида в пласте.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.