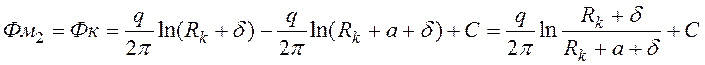 . (16)
. (16)
Из (15) и (16) :
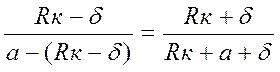 . (17)
. (17)
Откуда
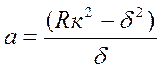 (18)
(18)
Для того чтобы определить дебит скважины А, запишем выражение потенциала на её забое:
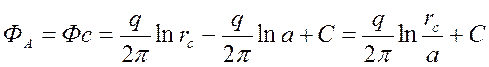 . (19)
. (19)
Вычитая (19) из (15) , получим:
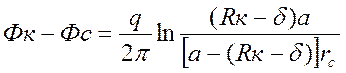 .
(20)
.
(20)
Подставляя (16) в (20) , получим :
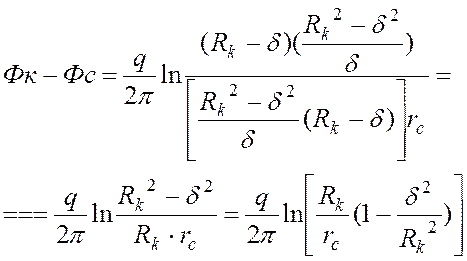 (21)
(21)
Из (21) дебит скважины:
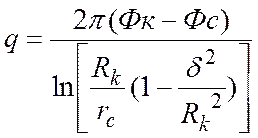 .
(22)
.
(22)
При эксцентриситете ![]() формула
(22) обращается в формулу Дюпюи.
формула
(22) обращается в формулу Дюпюи.
Потенциал в любой точке пласта М:
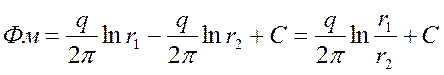 . (23)
. (23)
Вычитая из (23) (19) и учитывая (16) , получим:
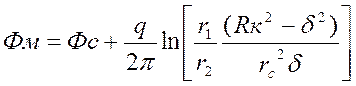 .
(24)
.
(24)
Скважина называется гидродинамически совершенной, если она вскрывает продуктивный пласт на всю толщину и забой скважины открытый, т.е. вся вскрытая поверхность забоя является фильтрующей.
§ Если скважина с открытым забоем вскрывает пласт не на всю толщину h,
а только на некоторую h, а только на некоторую глубину b, то ее называют
гидродинамически несовершенной по степени вскрытия пласта.
При этом 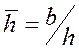 называется относительным вскрытием
пласта.
называется относительным вскрытием
пласта.
§ Если скважина вскрывает пласт до подошвы, но сообщение с пластом происходит только через специальные фильтры или отверстия в обсадной колонне или цементном кольце, то такую скважину называют гидродинамически несовершенной по характеру вскрытия пласта.
Как правило, реальные скважины имеют оба вида несовершенства, как по степени, так и по характеру вскрытия пласта.
Приток жидкости к несовершенным скважинам даже в горизонтальном однородном пласте перестает быть плоскорадиальным.
а) Если скважина выкрыла пласт неограниченной толщины на глубину b, то ее дебит можно рассчитать по формуле Гиринского Н.К. :
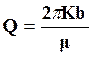
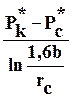 .
(1)
.
(1)
б) Пласт конечной толщины h.
Для расчета дебита скважины, несовершенной по степени вскрытия пласта, используется формула Н.Козени:
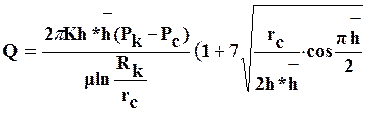 ). (2)
). (2)
Дебит несовершенной скважины удобно изучать, сравнивая ее дебит Q с дебитом совершенной скважины Qсов, находящейся в тех же условиях, что и данная несовершенная скважина. Гидродинамическое несовершенство скважины характеризуется коэффициентом совершенства скважины:
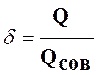 .
(4)
.
(4)
Для определения дебита гидродинамически несовершенных скважин в пластах конечной толщины предложена также универсальная формула:
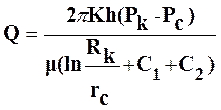 , (5)
, (5)
учитывающая как несовершенство по степени вскрытия (С1), так и по характеру вскрытия (С2).
С1 – дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия;
С2 - дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по характеру вскрытия.
Для С1 используется формула А.М.Пирвердяна:
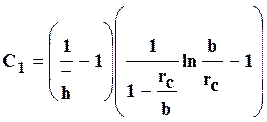 . (6)
. (6)
С2 зависит от:
§ числа перфорационных отверстий на один метр вскрытой породы пласта – n;
§ диаметра перфорационных отверстий dо ;
§ глубины проникновения пуль в породу – l'
§ диаметра скважины Дс;
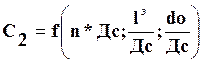 . (7)
. (7)
Параметры С1 и С2 можно найти из графиков В.И. Щурова, построенных по данным исследования притока жидкости к скважине на электролитических моделях (рис. 1, 2, 3, 4).
На рис. 12, 13, 14
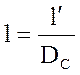 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.