Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 12

                                       

 

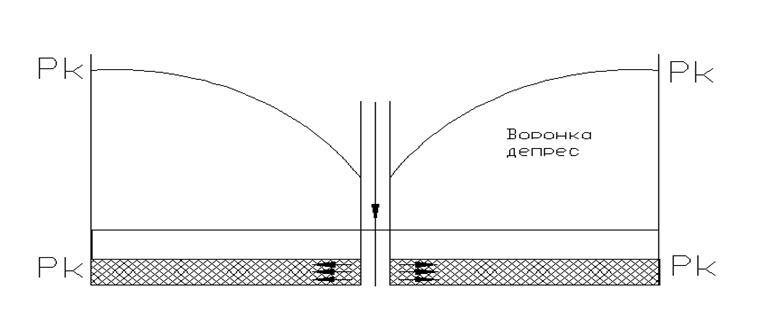
        R_к                                                               r                                R_к

График распределения давления в плоскорадиальном фильтрационном

                                              потоке.

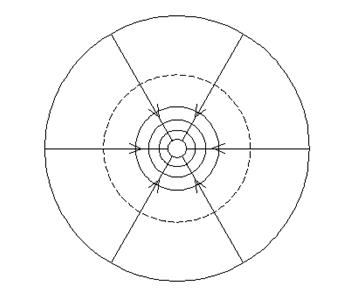
Гидродинамическое поле плоскорадиального фильтрационного потока.

                                                                  r

    График зависимости скорости фильтрации от расстояния до скважины.

   Отношение дебита скважины    к перепаду давления (депрессии)   называется коэффициентом продуктивности скважины:

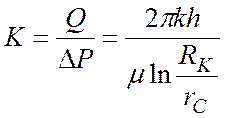                                         .                                          (36)

        График зависимости дебита   от перепада давления  называется индикаторной диаграммой.

       Все выведенные формулы справедливы и для нагнетания жидкости в пласт. В этом случае  и в формулы (25), (27), (28), (34) вместо  необходимо поставить .

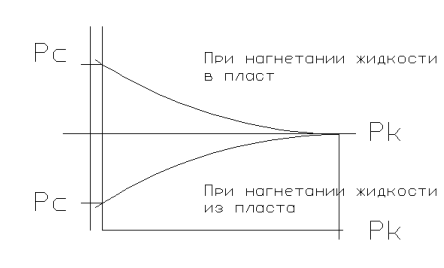
График распределения давления в пласте при нагнетании жидкости в пласт имеет вид:

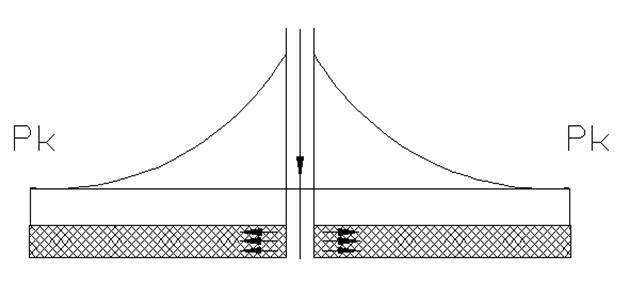
                                                               Р_С

  4.  Радиально-сферический фильтрационный поток.

В данном случае предполагается пласт неограниченной толщины с плоской горизонтальной непроницаемой кролей, через которую скважина сообщается с пластом полусферическим забоем. При эксплуатации такой скважины траектории движения всех частиц флюида в пласте будут прямолинейными и радиально-сходящимися к центру забоя.

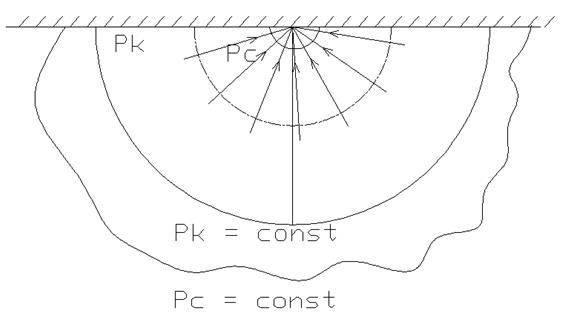Давление и скорость фильтрации будут функцией только расстояния до центра забоя, т.е. радиуса .

    .

На практике такой случай встречается, когда скважина вскрывает только кровлю пласта, а глубина вскрытия значительно меньше толщины пласта.

Уравнение Лапласа для потенциала скорости фильтрации в сферических координат:

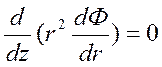                                          ;                                       (37)

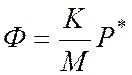,        где     ----  приведенное давление;

K = const;      = const.

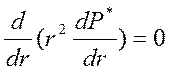                                               .                                    (38)

Интегрируя (38) по r  дважды,   получим:

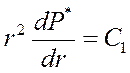
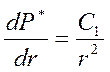                                или                  .           (39)

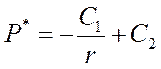                                                   .                                        (40)

 Граничные условия:                   

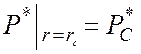
Таким образом:

                                                       .

 

                           .

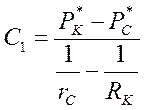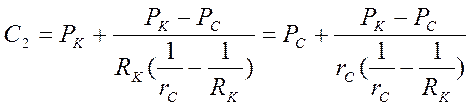         Подставляя постоянные  и  в (40) получим распределение давления в радиально-сферическом фильтрационном потоке несжимаемой жидкости: .

 При отборе жидкости из пласта: :

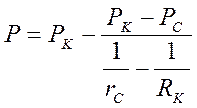                                  .                                             (41)

При нагнетании жидкости в пласт: :

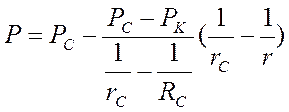                                    .                              (42)

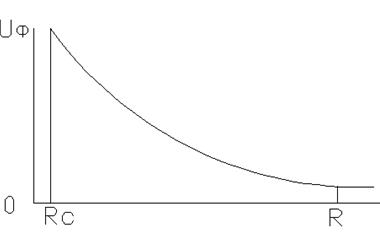
Графики зависимости  имеют вид  гиперболической кривой:

                          Р

                                                                         r

  Градиент давления:

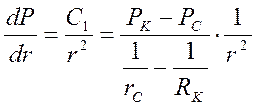                                               .                                  (43)

Скорость фильтрации

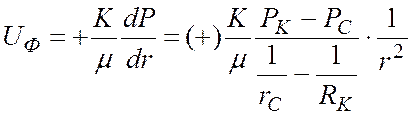                             .                         (44)

           Дебит добывающей скважины (т.е. расход жидкости через полусферическую поверхность радиуса ):