Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 11

 

Гидродинамическое поле фильтрационного потока --- совокупность изобар и линий тока (траекторий).           

       3.   Плоскорадиальный фильтрационный поток.

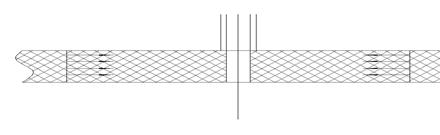
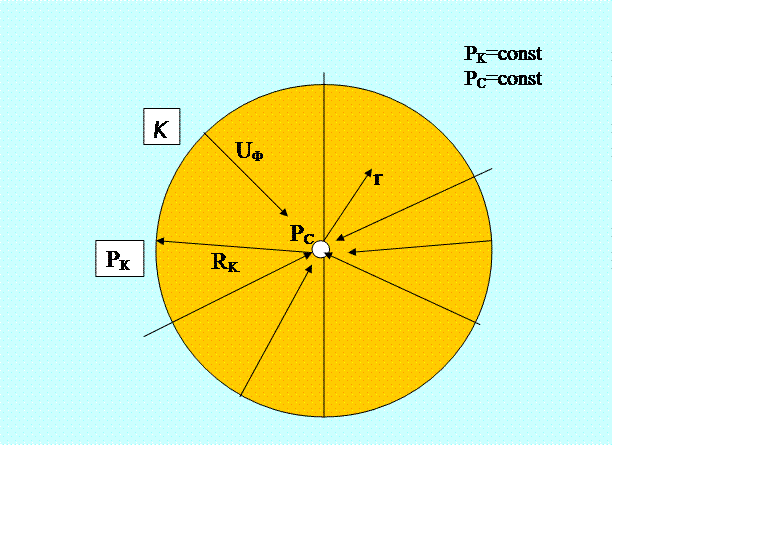
          Этот пример относятся к случаю горизонтального круглого пласта постоянной толщины, в центре которого пробурена одна скважина, вскрывшая пласт на всю толщину и имеющая открытый забой (т.е. вся поверхность забоя является открытой). Такая скважина называется гидродинамически совершенной.

          Радиус кругового пласта --- R_к. Внешней границей кругового пласта является контур питания  К,  на котором поддерживается постоянное давление  Р_К..    Радиус скважины ---  r. Давление на забое скважины  Р_С.

К = const;       = const.

 

         В данном случае

  давление и скорость фильтрации будут зависеть только от .

         Дифференциальное уравнение Лапласа в цилиндрической системе координат:

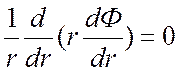                                                 .                                            (21)

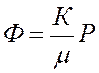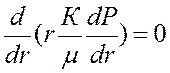                  .                         .                             (22)

Интегрируя (22),  получим:

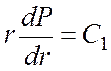                                                      ;                                                (23)

(24)

                               

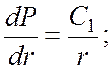
Граничные условия :                   .

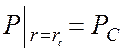Таким образом:                                                                                   

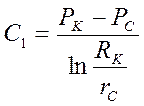
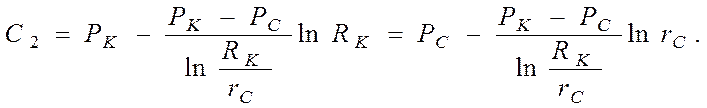
Следовательно:                      

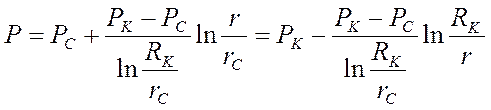             .                      (25)

Градиент давления:

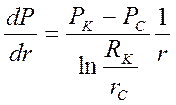                                             .                                             (26)

                      Скорость фильтрации:            

РU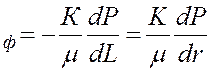.                         (27)                     

 

                             .

 

Таким образом: 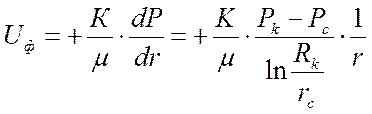            .                   (28)

(знак +  означает, что U противоположно r).

     Дебит скважины:

            Q = U_ф ·S(r ) = U2r h=

                                                          .

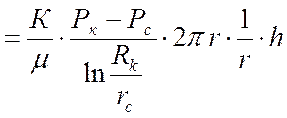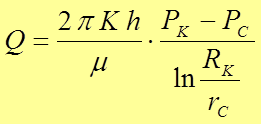                                          .                                      (29)

Формула (29) называется формулой Дюпюи.

        Определим закон движения частицы жидкости вдоль ее траектории.

Действительная скорость частицы жидкости:

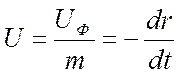                                                    .                                          (30)

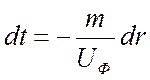                                                          .                                        (31)                             

Интегрируя (31) в пределах от  0  до  t  и от    до   ,  получим

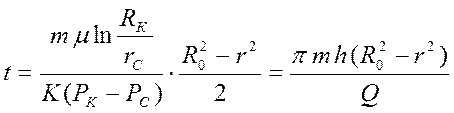                         .                    (32)

Время отбора всей жидкости из кругового пласта радиусом  получим, если вместо  подставим радиус контура питания , а вместо - радиус скважины :

                     

               .                                      (33)

Средневзвешенное по объему порового пространства пластовое давление:

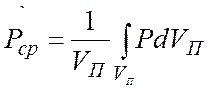                                            .                                         (34)

V_П --- объем порового пространства пласта:   
                                       .

Таким образом:

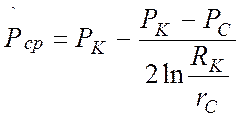                                 .                                              (35)

 

                                                             Р