Курс лекций по подземной гидромеханике: Учебное пособие по одноименному курсу, страница 30

                                 откуда         .                                                 (25)

    Равенство (25) показывает, что суммарная скорость  двухфазного потока ( а значит и суммарный расход  )  не зависят от координаты , а является либо постоянной, либо известной функцией времени.    

 (22) подставим в (25):

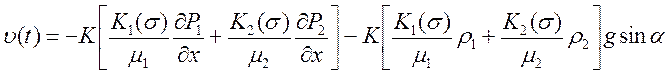  .       (26)

Из (26) исключим   с помощью равенства (24), продифференцированного по :

                             .

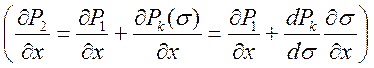После преобразований имеем:

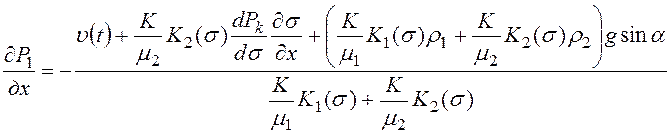      .    (27)

Подставляя (27) в 1-е уравнение (23) получим:

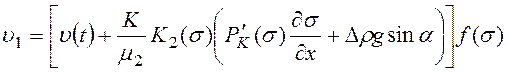                   ,                   (28)

     где: ; ; ; ;

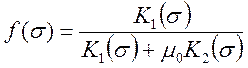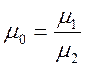Используя выражение (28) и уравнение неразрывности (22) для 1 фазы, окончательно получаем дифференциальное уравнение для определения насыщенности:

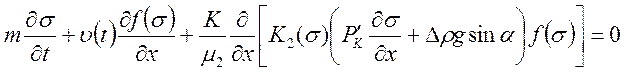         .        (29)

Если суммарная скорость фильтрации  постоянна: , то уравнение (29) можно упростить и перевести в безразмерный вид.

Введём безразмерные переменные: 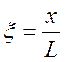   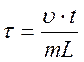              ;      ;                       (30)

где – характерный линейный размер (например, расстояние до эксплуатационной галереи).

Тогда с учётом (24) уравнение (29) принимает вид:

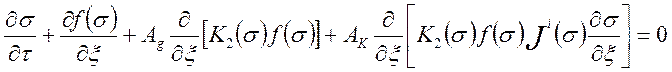.        (31)

где и – безразмерные параметры:

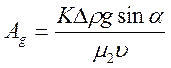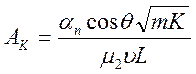                      ;        .                            (32)

Безразмерный параметр  характеризует отношение силы тяжести к силам вязкого трения.           Параметр – отношение капиллярных сил к силам вязкого трения.

    Если рассматривать вытеснение в пределах всего пласта и темпы вытеснения достаточно велики, то значения параметра  будут малы:  и капиллярными силами можно пренебречь

     Силой тяжести можно пренебречь, если , что имеет место при условии:                            .

   В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярными эффектами, а также влиянием силы тяжести, уравнение (31) приводится к виду:

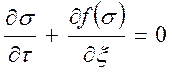                                               .                                              (33)

Т. к. 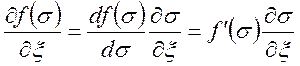     ,          то уравнение(33) запишем в виде:

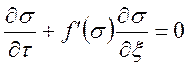                                             .                                            (34)

     Функция   называется функцией Баклея-Леверетта и характеризует распределение потоков фаз – отношение скорости фильтрации   вытесняющей фазы к суммарной скорости  .

 .

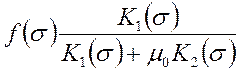                                ;              .                        (34а)

          Функция Баклея-Леверетта определяет полноту вытеснения и характер распределения насыщенности по пласту.

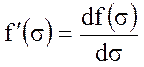 - производная от функции Баклея-Леверетта;

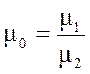 - относительный коэффициент вязкости.

Графики функции  Баклея-Леверетта f(σ) и ее производной  приведены на рис.1 и 2.

    Задачи повышения нефтеотдачи пласта в значительной степени сводятся к применению таких воздействий на пласт, которые изменяют вид функции  в направлении увеличения полноты вытеснения.

    Характерной особенностью функции Баклея-Леверетта  является наличие точки перегиба,  где вторая производная  соответственно больше или меньше нуля. Эта особенность определяет специфику фильтрационных задач вытеснения.

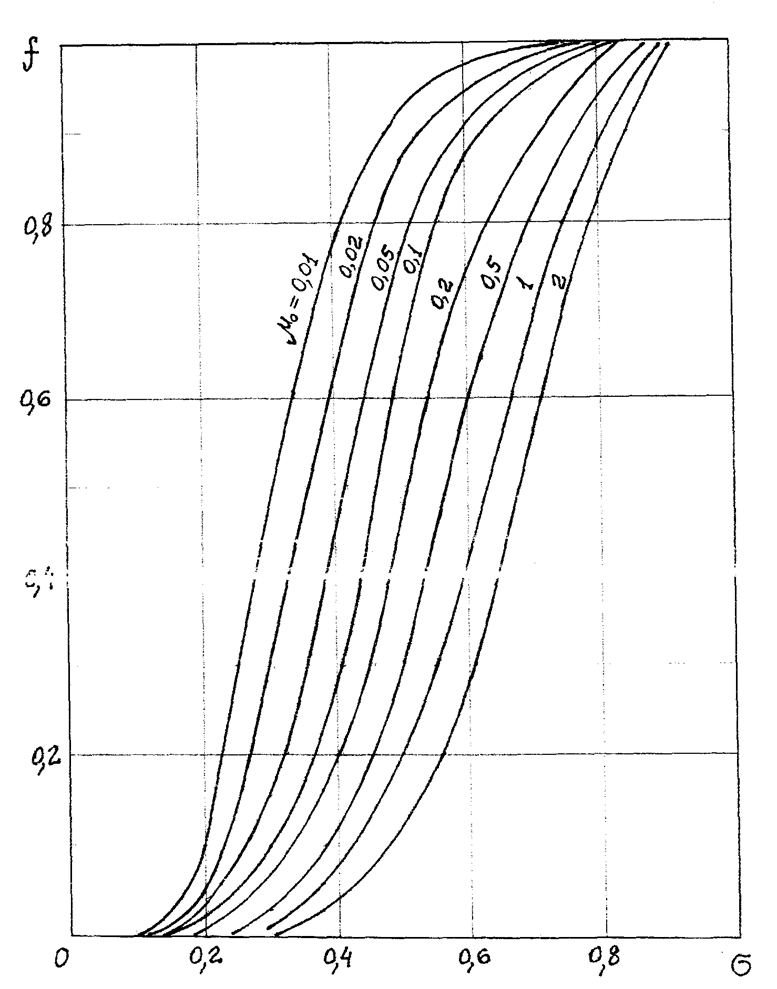
Рисунок 1.

График функции Леверетта f(σ)

σ – водонасыщенность порового пространства.

μ₀ – относительный коэффициент вязкости.

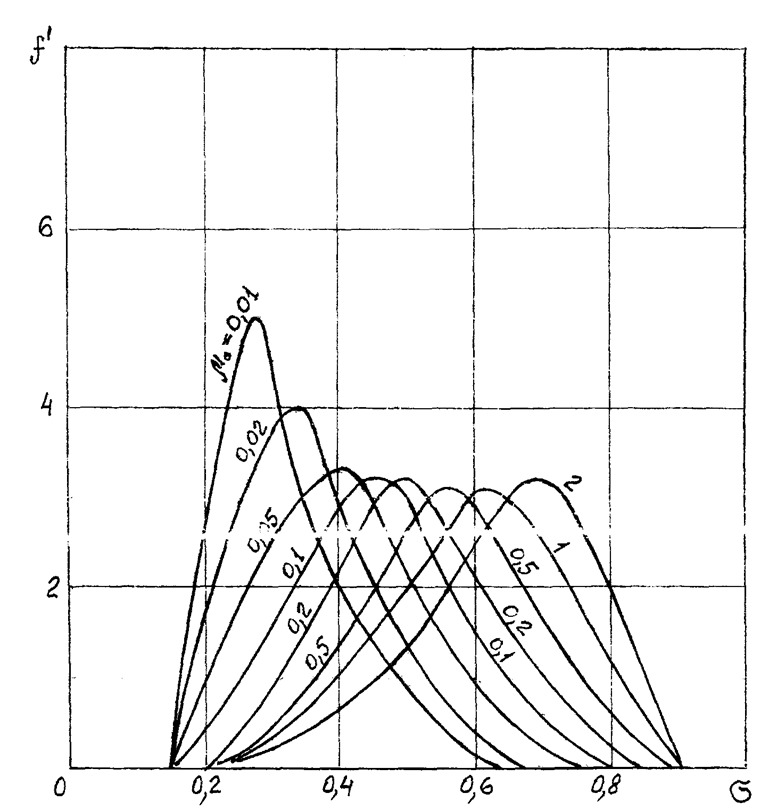
Рисунок 2.

График производной функции  Баклея- Леверетта    .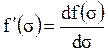

σ  – водонасыщенность порового пространства нефтяного пласта.

μ₀  –  относительный коэффициент вязкости воды.

    Используя графики  и  можно численными методами решить уравнение (34) и получить графическую зависимость . 

    Анализ  зависимости   показывает, что с течением времени  наклон кривых  становится круче и, наконец, в некоторый момент времени возникает разрыв (скачок) функции , т. е. движущейся вдоль  или  волны насыщенности вытесняющей фазы.