В силу уравнения неразрывности потока (т.е. закона сохранения массы), расход жидкости (дебит) постоянный и одинаков во всех зонах:
![]() .
.
Скорость фильтрации также будет постоянной и одинаковой во всех зонах.
|
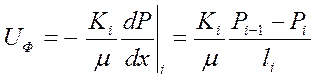 . (7)
. (7)
Выражение (7) для каждой зоны запишем в виде:
|
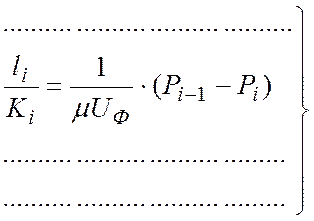 . (8)
. (8)
Просуммируем все выражения системы (8)
|
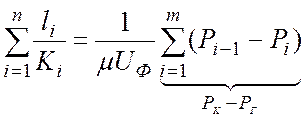 . (9)
. (9)
|
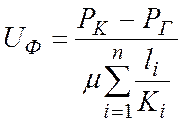 .
(10)
.
(10)
|
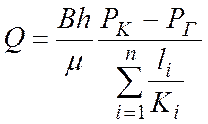 .
(11)
.
(11)
Следует иметь в виду, что действительные скорости движения частиц жидкости в разных зонах пласта будут различными:
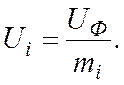
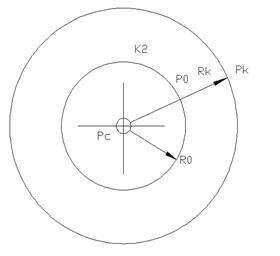
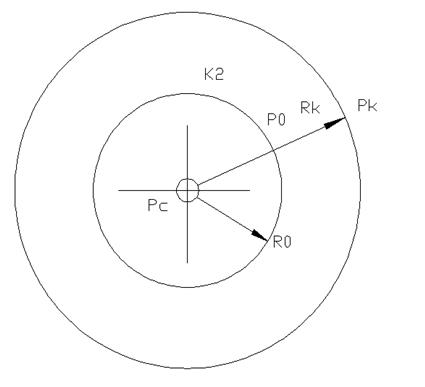
Если при плоскорадиальном притоке жидкости к гидродинамически совершенной скважине по закону Дарси зоны разной проницаемости имеют кольцеобразную форму, то формула дебита скважины для двухзонального пласта имеет вид:
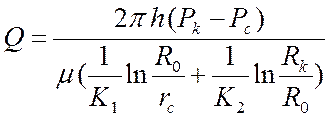 .
(12)
.
(12)
 |
|||
 |
|||
Распределение давления по зонам:
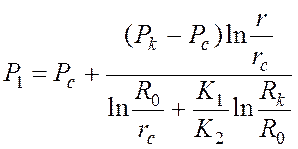 ;
; ![]()
![]() (13)
(13)
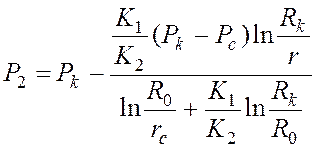 ;
; ![]() . (14)
. (14)
Возможен
случай, когда проницательность пласта в призабойной зоне является функцией ![]() :
: ![]() --- возрастает
или уменьшается от
--- возрастает
или уменьшается от ![]() ---- на забое скважины до
---- на забое скважины до ![]() на границе призабойной зоны
на границе призабойной зоны ![]() .
.
|
Если в призабойной зоне проницаемость изменяются линейно:
![]() ,
(15)
,
(15)
|
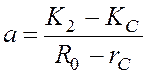 ,
, 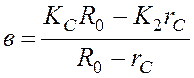 ,
,
то дебит скважины можно определить по формуле:
|
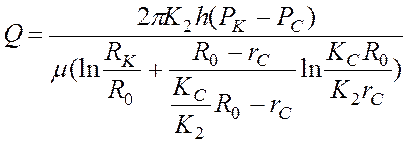 . (16)
. (16)
Рассмотрим прямолинейно-параллельный фильтрационный поток, фильтрация которого подчиняется нелинейному степенному закону:
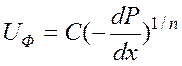 (
( ![]() )
, (1)
)
, (1)
где С и n – известные опытные константы.
Степенной нелинейный закон (1) описывает турбулентные режимы фильтрации.
Скорость фильтрации:
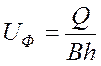
.
(2)
Из (1) и (2) получаем:
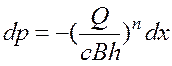 . (3)
. (3)
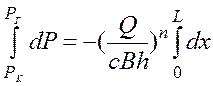 . (4)
. (4)
![]()
![]()
 Р
Р![]()
![]() Р
Р
Р![]()
h![]()
![]()
![]()
![]()
![]() Х
Х
0 х
Из (4) дебит потока:
Q= С(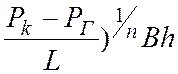 . (5)
. (5)
Проинтегрируем выражение (3) следующим образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.