b = ψbRl∙Rl [мм], полученное значение округляется до целого четного
20.6. Внешний делительный диаметр шестерни.
dl1 = mtl∙z1 [мм]
20.7. Средний делительный диаметр шестерни и колеса.
d1 = 0.857∙dl1; d2 = 0.857∙dl2 [мм]
20.8. Средний нормальный модуль.
mn = mtl∙(1 – 0.5 
) cos β [мм] где
β = 25˚ - для косозубых колес
β = 35˚ - для круговых зубьев.
20.9. Внешняя высота.
hl = 2mtl∙(cos β + 0.1) [мм]
20.10. Внешняя высота головки зуба.
hal1= mtl∙cos β [мм]
hal2 = 2∙ mtl∙cos β - hal1 [мм]
20.11. Внешняя высота ножки зуба.
hfl1 = hl - hal1 [мм]
hfl2 = hl - hal2 [мм]
20.12. Внешний диаметр вершин зубьев.
dal1 = dl1 + 2∙hae1∙cos δ1 [мм]
dal2 = dl2 + 2∙hae2∙cos δ2 [мм]
20.13. Средний нормальный модуль зубьев.
mn = 
[мм]
20.14. Коэффициент ширины шестерни по среднему диаметру.
ψbd = 
[мм]
20.15.Средняя окружная скорость колес.
υ = 
[м/с]
По скорости назначаем степень точности передачи (таблица 19.1)
Для проверки контактных напряжений определяем коэффициент нагрузки
КН = КНβ∙ КНα∙КНυ
КНα – коэффициент, учитывающий распределение нагрузки между зубьями (см. таблицу 14.5)
КНβ – коэффициент, учитывающий распределение нагрузки по длине зуба (см. таблицу 14.2)
КНυ – коэффициент, учитывающий динамическую нагрузку (см. таблицу 14.4)
20.16. Проверочный расчет по контактным напряжениям.
σН =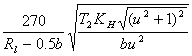 
≤ [σ]Н
недогрузка Δ = 
, до 10%
20.17. Сила в зацеплении.
Окружная сила
Ft1 = Ft2
= 
= 
[мм]
Радиальная сила для шестерни, равная осевой силе для колеса
Fr1 = Fa2 = Ft2(tg α cos δ1 + sin β sin δ1) [H]
Осевая сила для шестерни, равная радиальной силе для колеса
Fa1 = Fr2 = Ft2(tg α sin δ1 + sin β cos δ1) [H]
20.18. Проверка зубьев на выносливость по напряжениям изгиба.
σF = 
≤ [σF],
где
Ft – окружная сила
КF – коэффициент нагрузки
KFβ∙ KFυ
KFβ – коэффициент концентрации (см. таблицу 14.6.)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.