Методические указания к выполнению курсового проекта и расчётно-графических заданий по дисциплине «Деталям машин», страница 88

1.10.  Средний делительный диаметр шестерни и колеса
d₁=0,857∙d_l1=0,857∙64=54,85мм
d₂ = 0,857∙d_l2 = 0,857∙160 = 137,12 мм

1.11.  Внешние диаметры шестерни и колеса
d_ae1=d_e1+2m_lcosδ₁=64+2∙3,2∙cos21,8=70мм
d_ae2 = d_e1 + 2m_l cos δ₂ = 160 + 2∙3,2∙ cos 68,2 = 162,4 мм

1.12.  Средний окружной модуль
m =  =  = 2,74 мм

1.13.  Коэффициент ширины шестерни по среднему диаметру
ψ_bd =  =  = 0,47

1.14.  Средняя окружная скорость колес
V===4,м/с
По таблице 19.1 принимаем 8 степень точности
Коэффициент нагрузки
К_Н=К_Нβ∙К_Нα∙К_Нυ
К_Нα – коэффициент, учитывающий распределение нагрузки между прямыми зубьями, К_Нα=1,0
К_Нβ – коэффициент, учитывающий распределение нагрузки по длине зуба (см. табл. 14.2), К_Нβ=1,05
 К_Нυ = коэффициент, учитывающий динамическую нагрузку (см. табл. 14.4), К_Нυ=1,24
К_Н = 1,05∙1,0∙1,24 = 1,3

1.15.  Проверочный расчет по контактным напряжениям
σ_н2 = 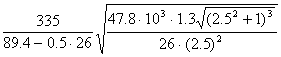 = 379 МПа

недогрузка Δ=  =  = 7,1% ≤ [10%]

1.16.  Силы в зацеплении

Окружная сила

F_t1 = F_t2 =  =  = 698 H

Радиальная сила для шестерни

F_r1 = F_a1 = F_t2∙tg α cos δ₁ = 698 ∙tg 20˚ ∙cos 21.8˚ = 236 H

Осевая для шестерни, равная радиальной для колеса

F_a1 = F_r2 = F_t2∙tg α sin δ₁ = 698 ∙tg 20˚ ∙sin 21.8˚ = 94 H

1.17.  Проверка зубьев на выносливость по напряжениям изгиба
σ_F=≤[σ]_F
K_F–коэффициент нагрузки
K_F=K_Fβ∙K_Fυ=1.08∙1.38=1.49
K_Fβ – коэффициент концентрации (см. таблицу 14.6), K_Fβ = 1,08
K_Fυ – коэффициент динамичности (см. таблицу 14.7), K_Fυ = 1,38
Y_F – коэффициент формы зуба, выбираем в зависимости от эквивалентных чисел зубьев:
для шестерни Z_v1===21,6
для колеса Z_v2===135,1
По эквивалентному числу зубьев определяется коэффициент формы зуба Y_F (см. таблицу 19.4.1)
Y_F1 =4,05;           Y_F2=1,60
находим отношение :
для шестерни ==58,5
для колеса ==57,2
Дальнейший расчет ведем для зубьев колеса, так как отношение меньше
σ_F2=≤[σ_F2]
σ_F2 =  = 52.6 МПа ≤ [σ_F2]  = 206 МПа