1.Гармонические колебания. Характеристики и формы представления.
Гармонические колебания
В общем случае состояние системы изменяется. Если в изменение обнаруживается повторяемость, то в системе происходят колебания. Если колебания повторяются через строго определенный промежуток времени, то такое колебание периодическое, а сам промежуток – это период Т. Колебания, происходящие по закону Sin или Cos называются гармоническими.
Причины гармонических колебаний:
Уравнение
гармонического колебательного движения имеет вид 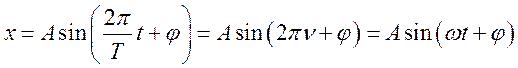 , где
, где ![]() - смещение точки от положения
равновесия, разное для разных моментов времени,
- смещение точки от положения
равновесия, разное для разных моментов времени, ![]() - амплитуда,
- амплитуда, ![]() -
период,
-
период, ![]() -
начальная фаза,
-
начальная фаза, ![]() -
частота колебаний,
-
частота колебаний, ![]() -
круговая частота. Скорость и ускорение точки, совершающей колебание,
определяются соотношениями
-
круговая частота. Скорость и ускорение точки, совершающей колебание,
определяются соотношениями 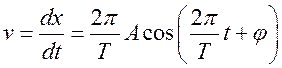 ,
,
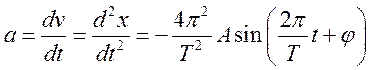 .
Сила, под действием которой точка массой
.
Сила, под действием которой точка массой ![]() совершает гармоническое
колебание,
совершает гармоническое
колебание, 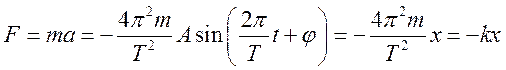 ,
где
,
где ![]() ,
т.е.
,
т.е. ![]() .
Здесь
.
Здесь ![]() -
период колебаний точки, совершающей колебания под действием силы
-
период колебаний точки, совершающей колебания под действием силы ![]() ,
где
,
где ![]() -
жесткость пружины, численно равная силе, вызывающей смещение, равное единице.
Кинетическая и потенциальная энергии колеблющейся точки имеют вид
-
жесткость пружины, численно равная силе, вызывающей смещение, равное единице.
Кинетическая и потенциальная энергии колеблющейся точки имеют вид 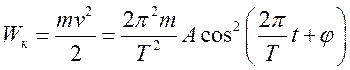 ,
,
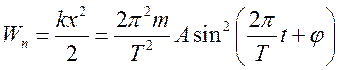 .
Полная энергия
.
Полная энергия 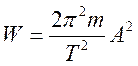 .
Примером гармонических колебательных движений могут служить малые колебания
маятника. Период колебаний математического маятника
.
Примером гармонических колебательных движений могут служить малые колебания
маятника. Период колебаний математического маятника ![]() .
.
Характеристики и способы представления гармонических колебаний
![]()
 x – смещение;
x – смещение;
A - амплитуда (максимальное значение x);
![]() - фаза;
- фаза;
![]() - начальная фаза, при t = 0, зависит от состояния система и времени;
- начальная фаза, при t = 0, зависит от состояния система и времени;
![]() - скорость изменения фазы с течением времени,
циклическая частота;
- скорость изменения фазы с течением времени,
циклическая частота;
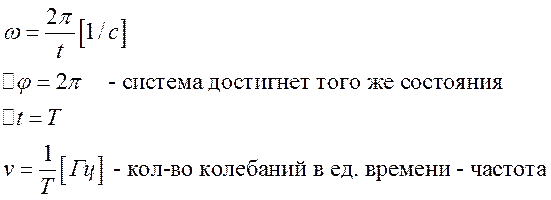
 Применяется для сложных
колебаний. Угловая скорость – циклическая частота.
Применяется для сложных
колебаний. Угловая скорость – циклическая частота.
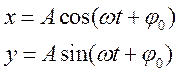

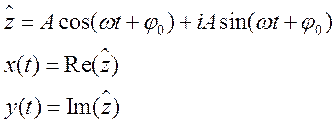
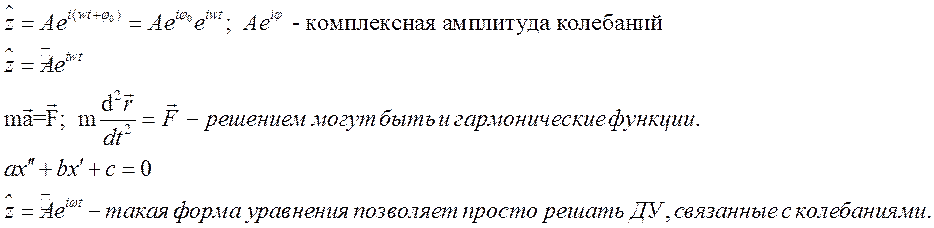
2.Сложение
однонаправленных колебаний. Векторные диаграммы. Биения.
При сложении двух
одинаково направленных гармонических колебаний одинакового периода получается
гармоническое колебание того же периода с амплитудой ![]() и с начальной фазой,
определяемой из уравнения
и с начальной фазой,
определяемой из уравнения 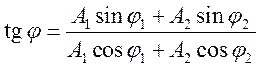 ,
где
,
где ![]() и
и
![]() -
амплитуды слагаемых колебаний,
-
амплитуды слагаемых колебаний, ![]() и
и
![]() -
их начальные фазы.
-
их начальные фазы.
1. Сложение однонаправленных колебаний с одинаковыми частотами:
Пусть система принимает участие в
двух однонаправленных колебаниях с одной ![]() .
.
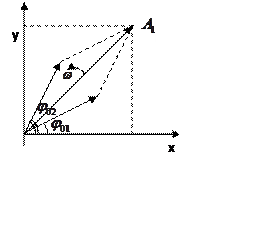

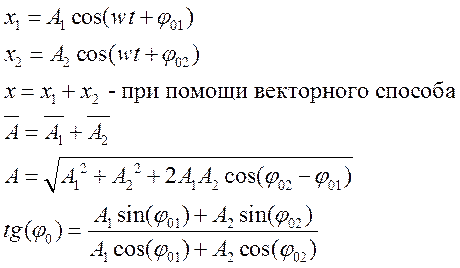
Сколько бы гармонических колебаний ни складывалось, получаем гармоническое колебание с такой же частотой, но у него своя амплитуда, которая зависит от амплитуды складываемых колебаний и от начальных фаз.
2. Сложение однонаправленных колебаний с разными частотами. Биения.
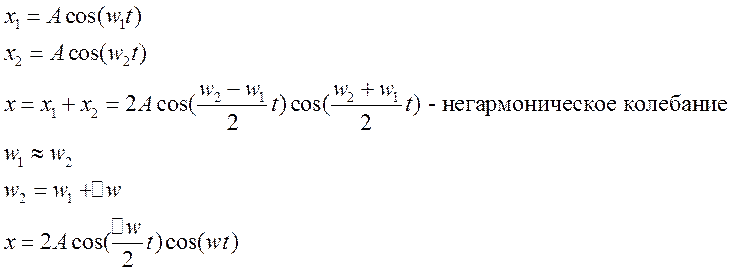
Результирующее x – это быстрое колебание с медленно изменяющейся амплитудой.
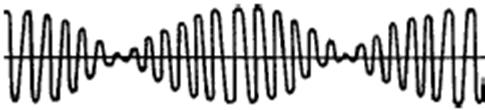
Если амплитуды разные, то нулевой амплитуды не получится. Если складываются колебания с разными частотами, то получаются не гармонические колебания.
3.Сложение перпендикулярных колебаний. Фигуры Лиссажу.
При сложении двух
взаимно перпендикулярных колебаний одинакового периода уравнение траектории
результирующего движения имеет вид 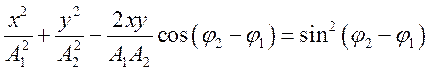 .
.
Сложение взаимно перпендикулярных колебаний
Разные 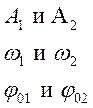
Результирующее движение в общем
случае сложное. Траектория может получиться не замкнутой. Замкнутая, если ![]() - кратны друг другу или частоты относятся,
как целые числа,
- кратны друг другу или частоты относятся,
как целые числа, 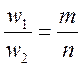 , тогда получится фигура Лиссажу.
, тогда получится фигура Лиссажу.
Пример:
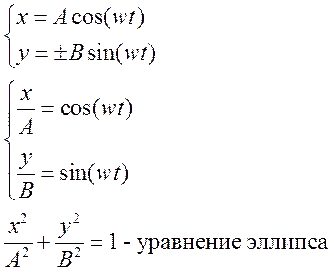
В общем случае фигура Лиссажу пересекает целое число раз каждую ось. Тогда частоты колебаний относятся между собой так, как относятся обратные числа:
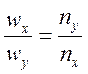

4.Гармонические осцилляторы. Дифференциальное уравнение гармонического осциллятора. Собственные колебания и энергия осциллятора.
Гармонические осцилляторы.
Среди любых систем можно выделить колебательную систему или осциллятор.
Такая система может совершать колебания сама по себе, те за счет внутренних причин, если у нее есть энергия. Если собственные колебания системы являются гармоническими то система- осциллятор.
Динамика гармонических колебаний описывается дифуром:
![]() (1)
(1)
Если для системы получается уравнение (1) то система – гармонический осциллятор.
![]() - собственная частота.
- собственная частота.
Дифференциальное уравнение гармонического осциллятора.
![]()
![]() =>
=> ![]() - решение этого уравнения есть функции вида
- решение этого уравнения есть функции вида
![]() ,
, ![]() .
.
Пример 1 (Пружинный маятник.)
![]()

![]()
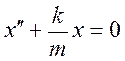
![]() - дифференциальное уравнение гармонического
осциллятора.
- дифференциальное уравнение гармонического
осциллятора.
![]()
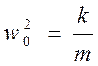
Решением
дифференциального уравнения будет![]() .
.
Величина собственной частоты зависит от свойств системы.
Причин колебаний 2:
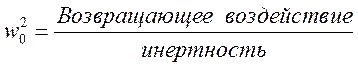
3 свойства осциллятора:
1. Начальное положение.
2. Возвращающая сила.
3. Инертность.
Пример 2 (Физический маятник).

 Равновесие
когда
Равновесие
когда ![]()
![]()
![]()
![]()
![]()
![]()
Если угол мал то:
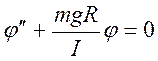
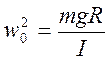 - собственная частота.
- собственная частота.
Пример 3 (Колебательный контур)
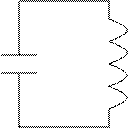 Сообщение заряда колебательному контуру выводит
систему из положения равновесия.
Сообщение заряда колебательному контуру выводит
систему из положения равновесия.
![]() - закон Кирхгофа.
- закон Кирхгофа.
![]()
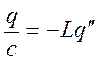 =>
=>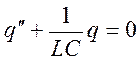
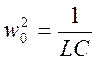
Возвращающие воздействие связанно с зарядом.
Энергия гармонического осциллятора.
Рассмотренные в примерах осцилляторы являются консервативными системами. Энергия с течением времени не меняется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.