 В реальных
квантовых системах образующие их микрочастицы тождественны (электроны не
отличаются друг от друга). Поэтому и в модельной макросистеме будем считать все
магниты тождественными. Нумеровать их не имеет смысла. Производящую функцию
можно записать так:
В реальных
квантовых системах образующие их микрочастицы тождественны (электроны не
отличаются друг от друга). Поэтому и в модельной макросистеме будем считать все
магниты тождественными. Нумеровать их не имеет смысла. Производящую функцию
можно записать так: ![]() - Бином Ньютона. [#
- Бином Ньютона. [#![]() ]. Для расчета состояний в общем случае
используют бином Ньютона:
]. Для расчета состояний в общем случае
используют бином Ньютона: ![]() =
= ![]() (N-число частиц системы, S-число
спинов, направленных вниз). На практике бином Ньютона записывается так:
(N-число частиц системы, S-число
спинов, направленных вниз). На практике бином Ньютона записывается так: ![]() =
=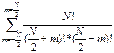 *
*![]() . В общем случае кол-во спинов направленных
вверх отличается от кол-ва спинов направленных вниз: m показывает, на сколько кол-во спинов, обращенных вверх
превышает кол-во спинов, обращенных вниз:
. В общем случае кол-во спинов направленных
вверх отличается от кол-ва спинов направленных вниз: m показывает, на сколько кол-во спинов, обращенных вверх
превышает кол-во спинов, обращенных вниз: ![]() ;
; ![]() . Величина равная 2m называется спиновым избытком. Она показывает сколько
спинов в конкретном состоянии не скомпенсировано. Зная спиновый избыток можно
найти суммарный магнитный момент системы:
. Величина равная 2m называется спиновым избытком. Она показывает сколько
спинов в конкретном состоянии не скомпенсировано. Зная спиновый избыток можно
найти суммарный магнитный момент системы: ![]() (Кол-во
нескомпенсированных спинов на магнитный момент первого спина). Введем
обозначение:
(Кол-во
нескомпенсированных спинов на магнитный момент первого спина). Введем
обозначение: ![]() . Коэффициент g показывает сколько различных
микросостояний имеют одно и тоже значение суммарного магнитного момента.
Поэтому g называют степенью вырождения
макросостояния. Наиболее вырожденным является макросостояние с нулевым
значением спинового избытка. Т.е. это такое макросостояние, в котором половина
спинов обращена вверх, а вторая половина – вниз. Как отмечено ранее, спины
самопроизвольно меняют свое направление. Поэтому макросистема постоянно
переходит из одного микросостояния в другое. Т.к. спины переворачиваются
независимо друг от друга, то каждое следующее микросостояние не зависит от
предыдущего. Степень вырождения разных макросостояний различна. Т.е. разные
макросостояния можно реализовать различным кол-вом микросостояний. Наиболее
часто в системе будет возникать то макросостояние, которое можно реализовать
наибольшим кол-вом способов. Следовательно, вероятность обнаружения
макросистемы в таком макросостоянии максимальна. Степень вырождения
макросистемы указывает на вероятность обнаружения системы в этом состоянии. Чем
больше вырождено макросостояние, тем больше вероятность его обнаружения. Для
модельной системы при отсутствии внешнего воздействия наиболее вероятным
является состояние, в котором половина спинов направлена в одну сторону, а
половина в другую. Другими словами: наиболее вероятно макросостояние, в котором
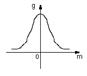
суммарный магнитный момент системы равен нулю. Вероятность обнаружения системы
с магнитным моментом не равным нулю значительно ниже. Вероятность обнаружения
системы в состоянии с магнитным моментом
. Коэффициент g показывает сколько различных
микросостояний имеют одно и тоже значение суммарного магнитного момента.
Поэтому g называют степенью вырождения
макросостояния. Наиболее вырожденным является макросостояние с нулевым
значением спинового избытка. Т.е. это такое макросостояние, в котором половина
спинов обращена вверх, а вторая половина – вниз. Как отмечено ранее, спины
самопроизвольно меняют свое направление. Поэтому макросистема постоянно
переходит из одного микросостояния в другое. Т.к. спины переворачиваются
независимо друг от друга, то каждое следующее микросостояние не зависит от
предыдущего. Степень вырождения разных макросостояний различна. Т.е. разные
макросостояния можно реализовать различным кол-вом микросостояний. Наиболее
часто в системе будет возникать то макросостояние, которое можно реализовать
наибольшим кол-вом способов. Следовательно, вероятность обнаружения
макросистемы в таком макросостоянии максимальна. Степень вырождения
макросистемы указывает на вероятность обнаружения системы в этом состоянии. Чем
больше вырождено макросостояние, тем больше вероятность его обнаружения. Для
модельной системы при отсутствии внешнего воздействия наиболее вероятным
является состояние, в котором половина спинов направлена в одну сторону, а
половина в другую. Другими словами: наиболее вероятно макросостояние, в котором
суммарный магнитный момент системы равен нулю. Вероятность обнаружения системы
с магнитным моментом не равным нулю значительно ниже. Вероятность обнаружения
системы в состоянии с магнитным моментом ![]() или
или ![]() мала, но не равна нулю.
мала, но не равна нулю.
4.5 Доступные состояния макросистемы.
В общ.случае макр-ние макросистемы – вырожденное =>его можно реализовать несколькими способами. Др. словами, каждому макросостоянию отвечают неск-ко микросостояний. Кол-во этих микросостояний = степени вырождения макросостояния. Все микросостояния, соответствующие одному макросостоянию, имеют одинаковый спиновый избыток. Это означает: энергия разных микросостояний одного макросостояния одинакова. Спины модельной макросистемы способны самопроизвольно менять своё направление =>система в одном микр-нии будет самопр-но переходить из одного микр-ния в другое. При этом спиновый избыток и состояние макр-мы не изменятся. Все микр-ния мак-мы с одинаковыми значениями энергии – доступные. Название обусловлено тем, что система в неизменных условиях может сапр-но оказаться в любом из этих микр-ний, т.е. каждое из этих микр-ний ей доступно. Пример: пусть модельная макр-ма состоит из 4х спинов: 3 вверх и 1 вниз. Возможны 4 разных микр-ния для этой системы. (нарисовать 4 комбинации из 4х стрелочек). У всех этих микр-ний одинаковый спиновый избыток => энергия системы в любом из этих состояний (система нах-ся в магнитном поле) одинакова => это доступные состояния системы. Другие возможные микр-ния макр-ме недоступны. Другие станут доступными при изменении условий существования системы (другое магн. поле).
4.6 Постулаты стат. физики.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.