2) ![]() =>
=> 
![]()
 Отраженная волна имеет ту же амплитуду, что и
падающая. Волны
будут противофазными.
Отраженная волна имеет ту же амплитуду, что и
падающая. Волны
будут противофазными.
3)
![]() =>
=>
![]()
![]()
13.Стоячие волны на струне.
Это частный случай явления интерференции волн.
Интерференция волн – перераспределение энергии в пространстве связанное со сложением нескольких когерентных волн.
У когерентных волн одинаковые частоты колебаний и неменяющиеся со временем разности фаз.
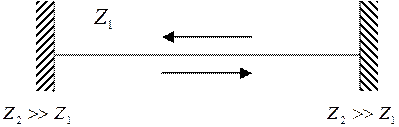 Если
по струне распространяется волна то результирующий волновой процесс есть сумма
прямой и отраженной волны.
Если
по струне распространяется волна то результирующий волновой процесс есть сумма
прямой и отраженной волны.
Если
![]() - пряма волна то
- пряма волна то ![]() - обратная волна.
- обратная волна.
![]()
![]() -
уравнение стоячей волны для поперечных волн на струне.
-
уравнение стоячей волны для поперечных волн на струне.
Воспользуемся граничными условиями.
![]()
![]()
![]()
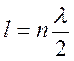 - условие существования стоячей волны.
- условие существования стоячей волны.
Стоячие
волны могут существовать на струне <=> когда на струне укладывается целое
число ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
14.Поперечные упругие волны на дискретной струне. Фазовая и групповая скорости волн. Дисперсия.
 Вещество, в том числе и струна, это среда дискретная,
в конечном счете она состоит из атомов. Если струна непрерывна, то на ней могут
существовать волны любой длины.
Вещество, в том числе и струна, это среда дискретная,
в конечном счете она состоит из атомов. Если струна непрерывна, то на ней могут
существовать волны любой длины.
Масса шариков одинакова и располагаются они одинаково Þдискретная струна характеризуется двумя параметрами: массой и периодом.
l min=2a
min=2a
гармоническая волна
Если среда дискретная, то в ней наблюдается дисперсия волн, которая выражается в том, что w(k)!=Vф. Vф!=const, k – не линейная функция.
![]() Применяем второй закон Ньютона для участка струны.
Применяем второй закон Ньютона для участка струны.
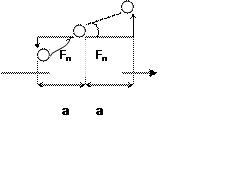
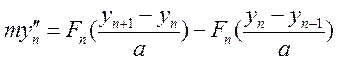
 - (*)
волновое уравнение для дискретной струны
- (*)
волновое уравнение для дискретной струны
имеет дифференционно-разностную природу.
yn(t)=Aei(wt-kx)=Aei(wt-kna)
![]() (**)
(**)
сделав подстановку (**) в (*), получили: 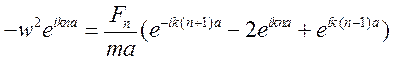

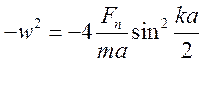
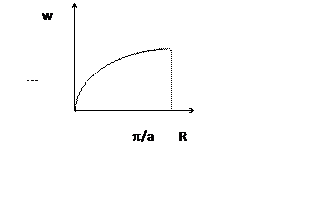
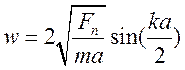 на величину циклической частоты
накладывается ограничение.
на величину циклической частоты
накладывается ограничение.
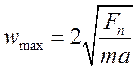
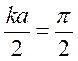 à
à 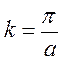
à 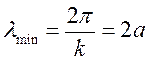
Максимальное значение частоты представляет собой собственную частоту противофазных колебаний соответствующих самой
маленькой длине волны.
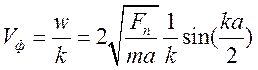 Þ
Þ 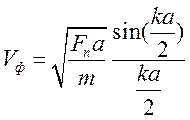 ,
, 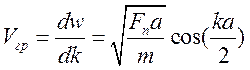
1)Низкие частоты: w->0, k->0
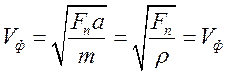 фазовая
скорость для непрерывной струны, где
фазовая
скорость для непрерывной струны, где 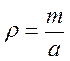 .
.
Изломы не играют роли (системы не ощущает своей дискретности)
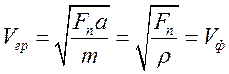 непрерывной
струны.
непрерывной
струны.
2) высокие частоты : w->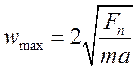 , k->
, k->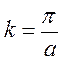
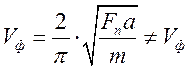 низкие
частоты. ÞВолновой пакет при такой волне будет деформироваться.
Волны с низкой частотой будут распространяться с «обычной » скоростью. Волны с
высокой частотой будут распространяться более медленно.
низкие
частоты. ÞВолновой пакет при такой волне будет деформироваться.
Волны с низкой частотой будут распространяться с «обычной » скоростью. Волны с
высокой частотой будут распространяться более медленно.
![]() переноса
энергии нет. à стоячая волна.
переноса
энергии нет. à стоячая волна.
Если система дискретна, она ведет себя как дискретная струна. Такие системы характеризует дисперсия.
15.Волновое управление для электромагнитных волн. Плоские гармонические волны и их характеристики.
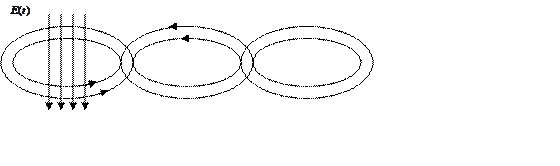
Электромагнитные волны представляют собой распространяющиеся в пространстве колебания электромагнитного поля. Источник – движущиеся заряды. В качестве исходного уравнения будем использовать уравнение Максвелла, в которое входит временное изменение полей.

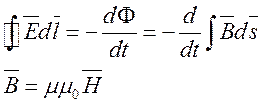
Электромагнитное
поле характеризуется векторами ![]() , а физическим смыслом
обладают векторы
, а физическим смыслом
обладают векторы ![]() .
.
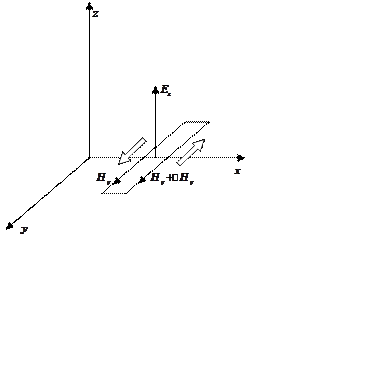
Получим волновое уравнение для случая плоских волн.
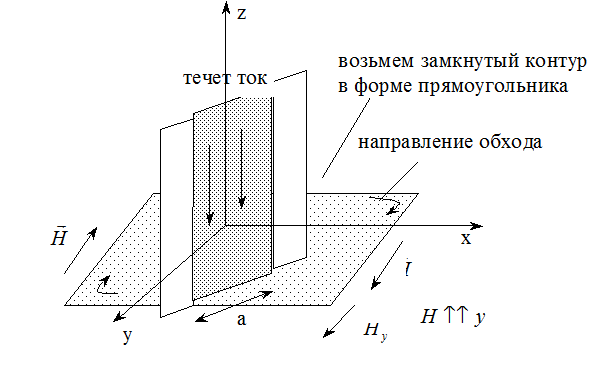
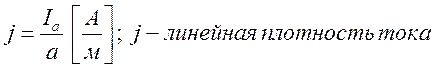
![]()
За счет этого поля появляется магнитное поле.
Уменьшим ширину по x прямоугольника в плоскости xy.
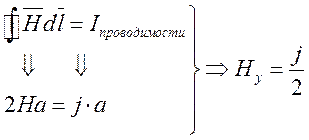 -
проекция H на ось y.
-
проекция H на ось y. 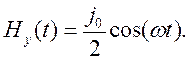
Силовые
линии должны быть перпендикулярны вектору ![]()
Пусть в пространстве непроводящая среда, т.е. удельная проводимость = 0.
Среду
будем характеризовать ![]() .
.
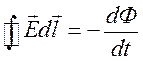 .
Изменение магнитного поля
.
Изменение магнитного поля ![]() возникает электрическое
поле.
возникает электрическое
поле. ![]() .
.
|

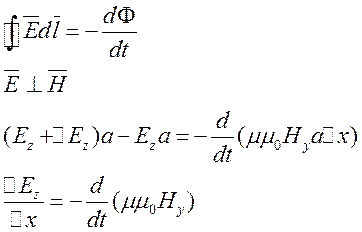
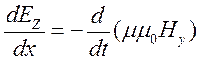 -
связь меняющегося магнитного поля и электрического поля.
-
связь меняющегося магнитного поля и электрического поля.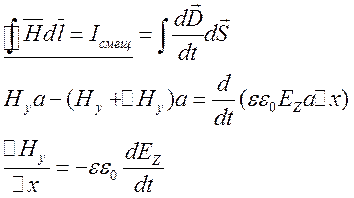
|
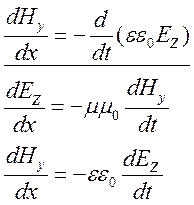 - связи между меняющимися
полями
- связи между меняющимися
полями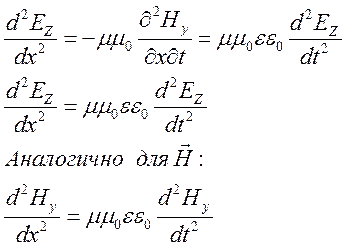 -
волновые уравнения
-
волновые уравнения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.