
![]() =0,
при выполнении этого условия явление резонанса исчезает. Если трение велико, то
резонанса не будет.
=0,
при выполнении этого условия явление резонанса исчезает. Если трение велико, то
резонанса не будет.
8.Явление резонанса. Резонанс смещения и резонанс скорости.
Резонанс скорости
х=Acos(wt+jo)
v=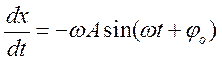
vA=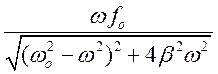
1) ![]() низкие
частоты.
низкие
частоты.
![]() ,
т.е. движения нет.
,
т.е. движения нет.
2) ![]()
![]()
Между w и vA должен быть максимум, следовательно резонанс скорости должен быть при любом значении трения.
VA=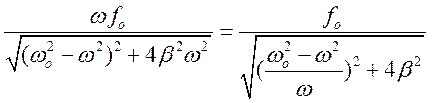
Скорость будет максимальной, когда частота вынужденного воздействия равна собственной частоте.
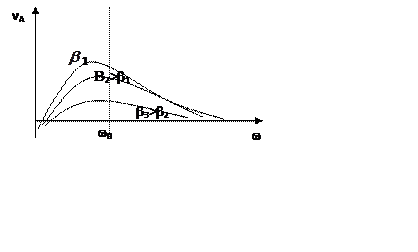 Резонанс скорости
существует всегда при любом трении.
Резонанс скорости
существует всегда при любом трении.
От резонанса скорости в принципе нельзя избавиться, также существует резонанс ускорения.
 В условиях малого можно
считать, что все частоты приблизительно равны 0.
В условиях малого можно
считать, что все частоты приблизительно равны 0.
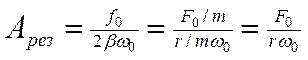
Фаза вынужденных колебаний.
F
= F0cos(t),
x = Acos(t+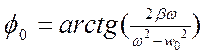
1) =0, 0=0
2) При произвольной частоте 0<0, т.е. колебания которые установятся в этой системе будут отставать по фазе от колебания воздействия.
=
-
характерная точка. В этом случае max
одной системы приходится на 0 в другой и наоборот. F
= F0cos(t),
x = Acos(t
- /2)
=
-
характерная точка. В этом случае max
одной системы приходится на 0 в другой и наоборот. F
= F0cos(t),
x = Acos(t
- /2)
Добротность и резонансные свойства системы
Резонансные свойства системы можно характеризовать добротностью.
 Арез –
резонансная частота
Арез –
резонансная частота
Аст – статическое смещение
1)
Аст
, когда w = 0;
Аст=![]()
2)
Арез,
когда w= wо;
Арез=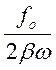
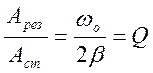 ;
;
![]() - ширина кривой
- ширина кривой
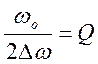 - добротность
характеризует меру ширины резонансной кривой.
- добротность
характеризует меру ширины резонансной кривой.
9.Импеданс колебательной системы. Анализ вынужденных колебаний с помощью импеданса.
Импеданс (полное сопротивление колебательной системы)
Для колебательного контура можно ввести величину импеданса:
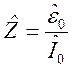 = R+i(wL-1/(wC))
= R+i(wL-1/(wC))
Z=![]() =R+i(wL-1/(wC))
=R+i(wL-1/(wC))
![]()
1) ![]() – связана с потерями энергии в контуре
– связана с потерями энергии в контуре
2) Im(![]() )= wL-1/(wC – реактивное
сопротивление, связано с запасами энергии.
)= wL-1/(wC – реактивное
сопротивление, связано с запасами энергии.
Величину импеданса можно ввести и для механической системы, например, пружинный маятник:
Z=r+i(wm-k/w)
10.Плоские гармонические волны и их характеристики. Фазовая и групповая скорости волн. Волновое уравнение.
Под волнами понимают процессы распространения в пространстве возмущений вещества или поля, сопровождаемые переносом энергии, а иногда и информации.
Волны могут иметь разную физическую природу. Пример таких волн: электромагнитные и акустические.
По мере того как возмущения распространяются, можно выделить поверхность в пространстве (до точек этой поверхности дошло возмущение). Эта поверхность называется волновым фронтом. Геометрия фронта зависит от ряда факторов. Главными из них являются:
1. геометрия источника
2. спектральный состав возмущения
3. среда (её неоднородности)
Þ Несколько видов волн:
1. Плоские волны 2. Сферические волны 3. Цилиндрические волны
 |
 |
||||
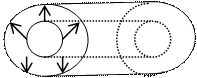 |
|||||
· ![]() Упругие
волны – распространяющиеся
в упругой среде механические возмущения (деформации). Внешние тела, вызывающие
эти возмущения в среде, называются источником волн. Распространение
упругих волн состоит в возбуждении колебаний всё более и более удаленных от
источника частиц среды. Важнейшее отличие упругих волн в среде от любого
другого упорядоченного движения её частиц состоит в том, что при малых
возмущениях (линейное приближение) распространение волн не связано с переносом
вещества.
Упругие
волны – распространяющиеся
в упругой среде механические возмущения (деформации). Внешние тела, вызывающие
эти возмущения в среде, называются источником волн. Распространение
упругих волн состоит в возбуждении колебаний всё более и более удаленных от
источника частиц среды. Важнейшее отличие упругих волн в среде от любого
другого упорядоченного движения её частиц состоит в том, что при малых
возмущениях (линейное приближение) распространение волн не связано с переносом
вещества.
 Упругая волна называется продольной,
если колебания частиц среды происходят в направлении распространения волны.
Упругая волна называется продольной,
если колебания частиц среды происходят в направлении распространения волны.
Упругая волна называется поперечной, если частицы среды колеблются в плоскостях, перпендикулярных к направлению распространения волны.
Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т.е. способна сопротивляться деформации сдвига. Этим свойством обладают лишь твердые тела. Продольные волны связаны с объёмной деформацией среды. Поэтому они могут распространяться как в твердых телах, так и в жидких или газообразных средах. Исключением из этого правила являются поверхностные волны, образующиеся на свободной поверхности жидкости или на поверхности раздела несмешивающихся жидкостей. При этом частицы жидкости одновременно совершают продольные и поперечные колебания, описывая эллиптические или более сложные траектории.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.