Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 28

Если колебания атомов в двухатомной молекуле происходят вдоль соединяющей их оси и достаточно просты для описания, то в многоатомных молекулах дело обстоит несколько сложнее. У них возможно одновременное возбуждение нескольких мод колебаний, количество и пространственная ориентация которых определяются числом внутренних степеней .свободы молекулы. Для молекулы произвольной конфигурации, состоящей из N атомов, это число равно 3N-6, для линейной молекулы, в которой все атомы расположены вдоль одной линии, оно равно 3N-5. В том и другом случае эта величина определяется как разность полного числа степеней свободы N материальных точек и суммы числа степеней свободы, связанных с поступательным и вращательным движением молекулы как целого. Разница состоит лишь в том. что у молекулы произвольной конфигурации число степеней свободы, связанное с вращением, равно 3 , а для линейной молекулы – 2. Поэтому сумма поступательных и вращательных степеней свободы в первом случае равна 6, а во втором – 5.

В многоатомных молекулах некоторые из колебательных мод определяют растяжение и сжатие межатомных связей вдоль линий, соединяющих атомы. Остальные колебательные моды описывают более сложные деформации молекул, например, изгибные.

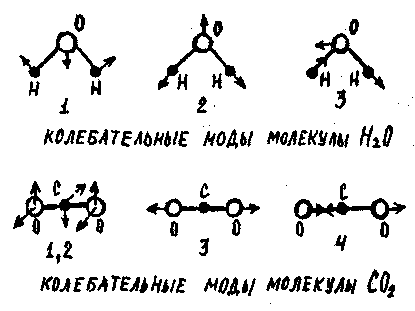На рис. показаны колебательные моды для двух молекул: воды Н₂О и углекислого газа CO₂.Молекула Н₂О является нелинейной и обладает 3N–6=3 степенями свободы, связанными с колебаниями. Следовательно, три моды характеризуют колебания этой молекулы. Первая мода является симметричным нагибным колебанием, вторая характеризует симметричное растяжение и сжатие молекулы вдоль направления связей, третья представляет собой асимметричную колебательную деформацию.

В отличие от Н₂О молекула СО₂ является линейной и обладает 3N–5=4 колебательными степенями свободы. Поэтому колебания данной молекулы связаны с четырьмя модами, первые две (1, 2) являются изгибными колебаниями, происходящими в двух взаимно перпендикулярных направлениях. Третья мода характеризует симметричное растяжение и сжатие вдоль направления связей, четвертая мода представляет собой асимметричное колебание вдоль направления связей.

В общем случае частоты и энергии различных мод различны, а сами колебательные моды существуют независимо друг от друга, одновременно определяя любое произвольное колебательное состояние молекулы.

Молекула также характеризуется степенями свободы, связанными с вращательным движением. Поэтому наряду с колебательными у молекул должны быть и вращательные энергетические состояния. Наиболее просто энергия таких состояний определяется для двухатомных молекул. Выделим ось, проходящую через центр масс молекулы перпендикулярно линии связи атомов. Момент инерции молекулы относительно этой оси может быть выражен через приведенную массу 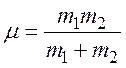 и расстояние между атомами R:

Энергия вращения молекулы относительно выделенной оси: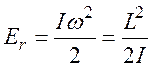

Момент импульса квантуется и может принимать лишь значения , определяемые квантовым числом l=0,1,2, ... Следовательно, энергия вращательного состояния тоже должна квантоваться, причем ее значения будут определяться величиной l: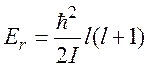

Как видно из последнего выражения, энергия вращательного состояния оказывается обратной моменту инерции молекулы. Следовательно, молекулы, обладающие малыми моментами инерции, будут иметь большие значения энергии вращательных состояний (при одних и тех же значениях l), чем молекулы с большими моментами инерции. Поэтому, чем меньше момент инерции молекулы, тем большая энергия требуется для возбуждения ее вращательных состояний. Именно по этой причине двухатомные молекулы (и любые другие линейные молекулы) практически не могут вращаться вокруг оси, проходящей через атомы. Момент инерции молекулы относительно такой оси оказывается исключительно малым. Поэтомy линейные молекулы, в отличие от молекул произвольной конфигурации, характеризуются не тремя, а двумя вращательными степенями свободы. Одна степень свободы, связанная с вращением относительно оси симметрии, оказывается энергетически недоступной.