Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 33

40.Равновесие системы в тепловом контакте. Температура. Энергия и температура.

Пусть 2 подсистемы I и II составляют замкнутую систему. Они могут обмениваться энергией .Полная энергия: .

 - число доступных состояний i-ой подсистемы. Число частиц и объемы подсистем – постоянны.

Доступные состояния газа определяются  только энергией и объемом сосуда,  и не зависят от квантовых состояний твердого тела. Найдем число доступных состояний замкнутой системы через  и .Будем комбинировать первое состояние из набора  с доступными состояниями из второго набора дает  доступных состояний замкнутой системы.

Для других состояний из первого набора – будет тот же результат.

 .

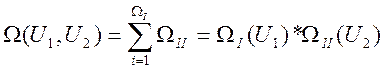Это функция должна быть максимальной(из постулатов), т.е.:

В другом виде: 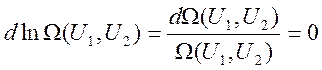          (1)

Прологарифмируем:    (2)

Тогда условие (1) примет вид:

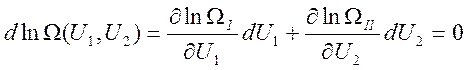
Условие замкнутости: , тогда:

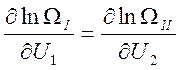 , т.к. это функции независимых переменных, то равенство такое может быть лишь тогда, когда они равны какой-то константе: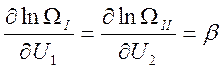

Необходимым и достаточным свойством равновесия систем в тепловом контакте является наличие общего для 2-х подсистем параметра .

Умножим (2) на множитель  и получим: . Энтропия составной системы равна сумме энтропий подсистем.

Другое условие равновесия: .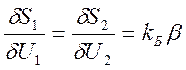

Введем новую физическую величину – температуру: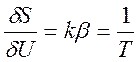

С учетом того, что температура вычисляется при постоянном числе частиц и постоянном объеме, то определение температуры примет вид: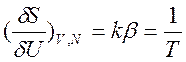

Рассмотрим 2 подсистемы, близкие к равновесию с T1 и Т2:

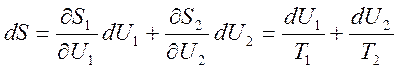
В равновесии энтропия максимальна, значит при переходе к равновесию dS>0. Пусть , учитывая , энтропия будет возрастать(dS>0), если  и

То энергия второй подсистемы увеличивается, а первой – уменьшается, то есть энергия(тепло) передается от подсистемы с большой температурой в подсистему с меньшей температурой.

41.Равновесие системы в диффузионном контакте. Химический потенциал. Химический потенциал и потоки частиц.

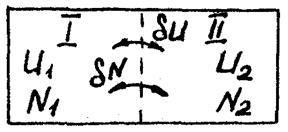Рассмотрим условия равновесия для двух подсистем, которые обмениваются не только энергией, но и частицами. Такой контакт называется диффузионным. Пусть подсистема I обладает энергией U₁ и числом частиц N₁, а подсистема II – энергией U₂ и числом частиц N₂ (см. рис.) Система из двух подсистем замкнута. То есть:

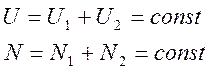
Обозначим через  и  число доступных состояний первой и второй подсистем, соответственно.

Число доступных состояний замкнутой системы определяется формулой

Условие максимума  принимает вид

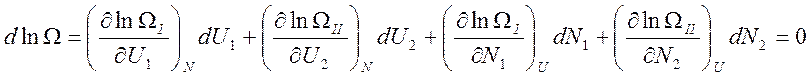
Равенство нулю последнего соотношения возможно при выполнении двух условий:

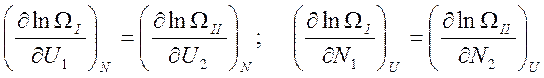
Первое условие известно и совпадает с  условием 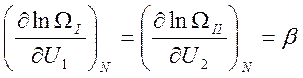. Второе – требует введения нового параметра: равновесия:

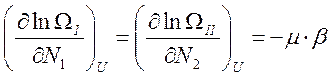
Параметр µ называется химическим потенциалом.

Через энтропию химический потенциал будет определяться формулой

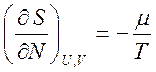
Рассмотрим теперь две подсистемы, близкие к равновесию с одинаковыми температурами, но разными химическими потенциалами. Энтропия замкнутой системы имеет вид

Вычислим полный дифференциал

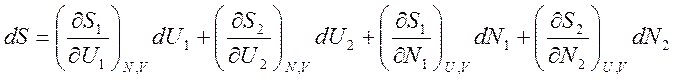
Учитывая, что 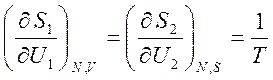, получаем

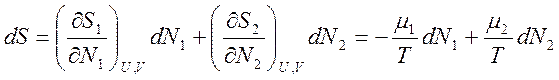
Пусть . Энтропия будет прирастать (), если  и . Это означает, что при переходе к равновесию частицы переходят из области с большим химическим потенциалом в область с меньшим химическим потенциалом.

42.Каноническое распределение Больцмана.

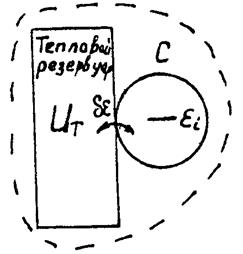
Пусть система С находится в квантовом состоянии с энергией ε_i (см. рис.). Полная энергия замкнутой макросистемы постоянна:

 Система С, переходя по состояниям, может быть обнаружена в них с различной вероятностью. Вычислим вероятность обнаружения системы С в квантовом состоянии с энергией ε_i. Для этого необходимо подсчитать число доступных состояний замкнутой   макросистемы , когда система С находится в i-м квантовом состоянии. Величина  определится только доступными состояниями термостата, так как i-е квантовое состояние системы С единственное. Обозначая  число доступных состояний термостата, получаем