Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 37

48.Идеальный газ. Статистика идеального газа. Химический потенциал идеального газа.

Рассмотрим газ, состоящий из не взаимодействующих между собой молекул, помещённых в прямоугольный объём с размерами Будем считать. что каждая из молекул находится в основном состоянии. Молекулы взаимодействуют со стенками сосуда, которые являются для них непрозрачными. Это означает, что для каждой молекулы рассматриваемый объём является трёхмерной бесконечно глубокой потенциальной ямой.

В природе существует только 2 сорта частиц- фермионы и бозоны, подчиняющиеся соответствующим статистикам Ферми-Дирака и Бозе-Энштейна.

В термодинамике и статистической физике идеальный газ известен как система частиц, описываемая законами классической механики, т.е. наличий у частиц спина никак не сказывается на них макроскопическом поведении. Значит, при квантово-механическом описании термин «идеальный газ» соответствует ограничению, накладываемому на систему частиц, а именно – макроскопическое поведение такой системы не должно зависеть от того, состоит она из бозонов или фермионов. Возможность такого описания реализуется при использовании квазиклассического распределения

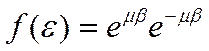          (1)

где

Обозначим величину  символом λ и запишем условие применимости распределения (1).

λ =<<1,                                       (2)

считая, что энергии орбиталей ε. Запишем уравнение, позволяющее определить хим. потенциал (или λ).

N=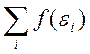                                   (3)

Где N- полное число частиц системы; - среднее число частиц на орбитали с энергией  и суммирование ведётся по всем орбиталям.

Суммирование в (3) можно заменить интегрированием, воспользовавшись плотностью состояний ρ(ε). Так, число квантовых состояний с энергией в пределах от ε до ε+dε будет представлено в виде ρ(ε)dε.

Среднее число частиц на каждой из этих орбиталей определяется величиной . Полное число частиц в интервале энергий от ε до ε+dε

dN= f(ε)ρ(ε)dS

Тогда, полное число частиц :     

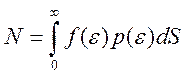
Возможность замены суммы обуславливаем тем, что для макроскопического объёма плотность состояний очень велика.

49.Внутренняя  энергия идеального газа.

Внутренняя энергия газа складывается из энергий частиц, его состовляющих. Число частиц с энергией от ε до ε+dε определяется формулой  dN=f(ε)ρ(ε)dS. Тогда энергия этих частиц

                               

Полная энергия системы (внутренняя энергия) определяется интегралом

                              

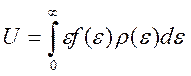
Подставляя в интеграл (2) соответствующие функции и произведя в интеграле замену переменных , получаем

                

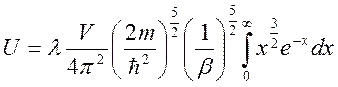
Интеграл 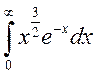 = 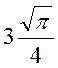. Тогда получаем

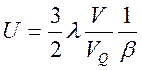
Учитывая, что 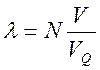 , , окончательно имеем

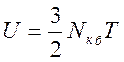                      (1)

Из (1) следует,что идеальный газ представляет собой набор частиц со средней энергией .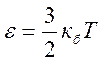

В статистической физике и термодинамике используется такая велична,как моль. Моль содержит N₀ = 6.022*10²³ молекул/моль и его масса численно равно молекуляной массе в граммах. Величина N₀  называется числом Авогадро.

R=N₀k_б  (универсальная газовая постоянная, 8.31 Дж/Кл*моль)

50.Уравнение состояния идеального газа.

Взаимодействие идеального газа с внешними телами определяется его давлением, которое можно вычислить из соотношения:

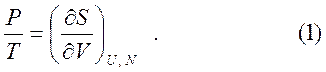
При постоянной внутренней энергии U и числе частиц N  формулу

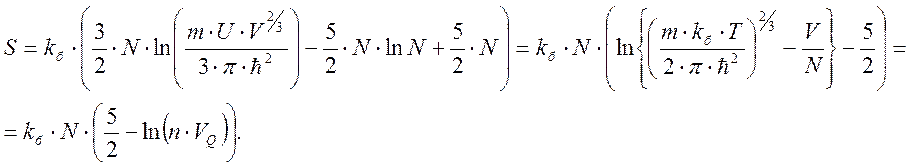удобно записать в виде

Вычисляя производную

             

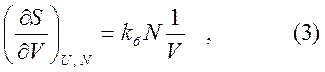
получаем

             

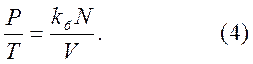
Перепишем формулу (4) в более привычной форме:

             

которая известна как уравнение состояния идеального газа или уравнение Менделеева-Клапейрона.

              Приведём ещё одну форму записи уравнения  (5):

             

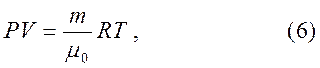
где m- масса газа; μ₀- масса моля газа; R- универсальная газовая постоянная.

              Уравнение Менделеева-Клапейрона однозначно определяет равновесное состояние идеального газа, связывая между собой макроскопические величины (объём, давление, количество вещества) с параметром термодинамического равновесия- температурой.