Как показывают расчеты, у атома водорода разность длин волн, соответствующая тонкой структуре спектров, приблизительно равна 1 Å. Даже для самой короткой длины волны спектра водорода эта величина составляет менее одной десятой процента.
Выводы
1. Состояния электрона в атоме водорода квантованы и
однозначно определяются значениями четверки квантовых чисел 
.
2. Если принимать во внимание только электростатическое взаимодействие электрона с ядром, то энергия атома водорода зависит только от главного квантового числа n. Любой энергетический уровень при этом имеет 2n2 – кратное вырождение.
3. Состояние с n=1 (1s-состояние) является основным для атома водорода, так как энергия этого состояния минимальна. Любые другие состояния являются возбужденными.
4. Переходы атома из возбужденных состояний в нижележащие
подчиняются правилу отбора 
и сопровождаются
испусканием фотонов, энергия которых определяется разностью энергий начального
и конечного состояний. Разрешенные частоты излучения могут принимать лишь
дискретные значения и образуют отдельные спектральные серии, связанные с
переходами в одно и то же нижележащее состояние.
5. Энергетические состояния и спектры атома водорода имеют тонкую структуру, связанную со спин-орбитальным взаимодействием.
Спин определяет коллективное поведение частиц. Частицы с нулевым или целым спином могут находиться в пределах данной системы в одинаковом состоянии в неограниченном количестве. Такие частицы называются бозонами. Можно сказать, что бозоны являются ”коллективистами”, они любят накапливаться в одном и том же состоянии. Частицы с полуцелым спином могут находиться в квантовых состояниях только по одиночке. Такие частицы называются фермионами.
Рассмотрим два электрона, взаимодействие которых достаточно
мало. Пусть каждый из них находится в некотором состоянии, характеризующимся
четверкой квантовых чисел( в том числе спином ). Обозначим эти состояния a и b. Тогда волновые функции,
соответствующие этим состояниям: 
. Возможны две ситуации:
1.
В состоянии с волновой функцией 
находится
1-ый электрон, а в состоянии с волновой функцией 
-второй.
Тогда двух частичная волновая функция 
может
быть представлена в виде произведения одночастичных функций, то есть
2.
Функция соответствует состоянию второго
электрона, а - первого.
Вследствие тождественности частиц:
.
Если выполняется первое соотношение (+), то волновая функция называется симметричной, если второе - антисимметричной.
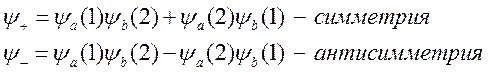
Вид функции( симметрия или антисимметрия )определяется спином частиц: для бозонов функция симметрична, для фермионов - антисимметрична.
При 
. Следовательно,
вероятность пребывания 2-х электронов в одном состоянии равна нулю. То же самое
справедливо и 2-х фермионов.
Принцип Паули.
В одном и том же состоянии не может находиться больше 1-ой частицы с полуцелым спином.
Если состояние характеризуется 4-ой квантовых чисел, то в системе не может быть 2-х или более фермионов с одинаковыми 4-мя квантовыми числами. Бозоны могут располагаться в произвольном количестве в любом состоянии. У электронов хотя бы одно число должно быть разным. В соответствии с принципом запрета происходит заполнение разрешенных состояний электронами в многоэлектронных системах.
Многоэлектронные атомы.
-система, в которой находятся несколько электронов.
Так же как и атом водорода, многоэлектронные атомы имеют ядро, в которое наряду с положительно заряженными протонами входят нейтроны, не имеющие электрического заряда. Количество протонов в ядре определяется атомным номером, а суммарное количество протонов и нейтронов – массовым числом. Поскольку атом нейтрален, то число электронов в нем строго равняется числу протонов и равно атомному номеру.
Таким образом, многоэлектронные атомы включают в себя несколько подсистем тождественных частиц. Рассмотрим электронную систему атома. Такая система полностью описывается многочастичной волновой функцией, которая зависит от координат и спинов всех электронов. Зная эту функцию, можно найти плотность вероятности распределения электронов в атоме. Однако определения конкретного вида самой функции является очень сложной задачей. Поэтому при анализе многоэлектронных атомов используется одноэлектронной приближение: предполагая, что все электроны в атоме не взаимодействуют получаем, что
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.