![]() , где
, где ![]() -координата
i-ой частицы, а
-координата
i-ой частицы, а ![]() -
волновая функция i-ой частицы.
-
волновая функция i-ой частицы.
После того, как одночастичные волновые функции в первом приближении найдены( когда взаимодействием электронов пренебрегаем ), можно учесть взаимодействие электронов. Зная волновые функции отдельных электронов, можно найти эффективное электрическое поле, которое они создают. Потенциал этого поля суммируется с потенциалом поля ядра и подставляется в уравнение Шрёдингера. Решение последнего позволяет найти одночастичные функции в новом приближении. Далее процедура многократно повторяется до тех пор, пока вид одночастичых функций практически перестанет меняться. В результате определено некоторое эффективное электрическое поле, в котором движется каждый электрон, и найдены волновые функции электронов, соответствующие этому полю.
В одноэлектронном приближении электронные состояния в
многоэлектронных атомах определяются 4-ой квантовых чисел:![]() . Энергия состояния зависит не только от
главного числа n, но и от орбитального квантового числа
. Энергия состояния зависит не только от
главного числа n, но и от орбитального квантового числа
![]() . Общая закономерность
состоит в том, что при фиксированном n величина энергии
растет с ростом
. Общая закономерность
состоит в том, что при фиксированном n величина энергии
растет с ростом ![]() .
.
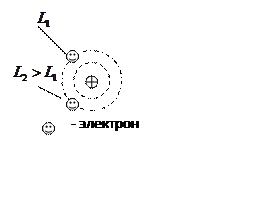 Возьмем несколько электронов с одинаковым n>1
и разным
Возьмем несколько электронов с одинаковым n>1
и разным ![]() . Орбитальный
механический момент:
. Орбитальный
механический момент: ![]() .
Чем больше L, тем больше импульс и тем дальше от ядра
электрон.
.
Чем больше L, тем больше импульс и тем дальше от ядра
электрон. ![]() находится в более глубокой потенциальной
яме. Для
находится в более глубокой потенциальной
яме. Для ![]() яма более пологая, так как заряд ядра
компенсируется электронами, которые ближе к ядру.
яма более пологая, так как заряд ядра
компенсируется электронами, которые ближе к ядру.
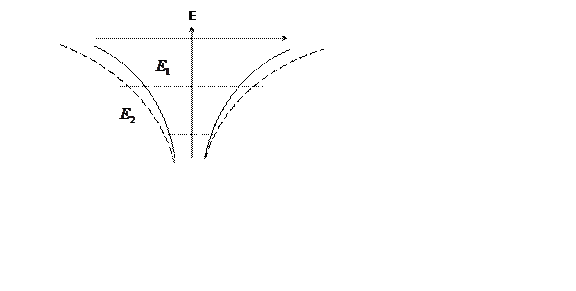
Пример. Типичная схема расположения энергетических уровней многоэлектронного атома.
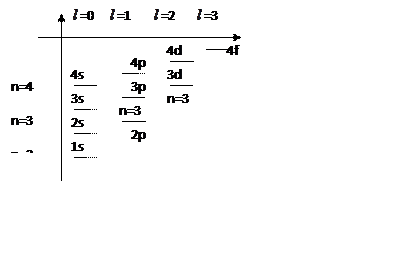 За счет зависимости энергии от орбитального квантового числа
некоторые уровни с большим n, но с меньшим
За счет зависимости энергии от орбитального квантового числа
некоторые уровни с большим n, но с меньшим ![]() оказываются лежать ниже, чем уровни
с меньшим n, но большим
оказываются лежать ниже, чем уровни
с меньшим n, но большим ![]() .Например, 4s(
n=4
.Например, 4s(
n=4 ![]() =0
) лежит ниже 3d( n=3
=0
) лежит ниже 3d( n=3 ![]() =0 ). Причиной периодичности свойств
элементов и связанных с этим горизонтальных периодов таблицы Менделеева
является повторяемость заполнения электронами некоторых близко расположенных
групп энергетических состояний, получивших название оболочек. Сходные
физико-химический свойства элементов, стоящих в одной группе таблицы,
связываются при этом с одинаковым заполнением внешних энергетических оболочек
различных атомов одной группы.
=0 ). Причиной периодичности свойств
элементов и связанных с этим горизонтальных периодов таблицы Менделеева
является повторяемость заполнения электронами некоторых близко расположенных
групп энергетических состояний, получивших название оболочек. Сходные
физико-химический свойства элементов, стоящих в одной группе таблицы,
связываются при этом с одинаковым заполнением внешних энергетических оболочек
различных атомов одной группы.
Заполнение электронных состояний в многоэлектронном атоме.
Рассмотрим атомы в невозбужденных состояниях. Тогда заполнение соответствует 2-м принципам:
1. С увеличением числа электронов у атомов, каждый “новый “ электрон должен занимать разрешенное состояние с наименьшей энергией. Если это не так, то энергия теряется в виде фотонов.
2. Принцип запрета Паули.
Заполнение идет снизу, начиная с 15-ого состояния. В 15-ом состоянии может находиться только два электрона с разными спинами.
 Структура уровней в многоэлектронных атомах является многооболочечной.
Электронные оболочки: n=1,2,3... Внутри каждой оболочки
есть оболочки с различными
Структура уровней в многоэлектронных атомах является многооболочечной.
Электронные оболочки: n=1,2,3... Внутри каждой оболочки
есть оболочки с различными ![]() =0,
=0,![]() 1,.... Любая оболочка может быть
пустой, заполненной, либо заполненной частично. Самая верхняя, содержащая
электроны называется валентной( внешней ). Электроны в ней валентные.
Электронам в обычных условиях необходима энергия-
1,.... Любая оболочка может быть
пустой, заполненной, либо заполненной частично. Самая верхняя, содержащая
электроны называется валентной( внешней ). Электроны в ней валентные.
Электронам в обычных условиях необходима энергия-![]() , чтобы
перейти в другую электронную оболочку. Атомы с полностью заполненной внешней
оболочкой наиболее устойчивы. Они, как правило, в хим. реакции( без спец.
условий ) не вступают. Такими системами являются атомы инертных газов. Атомы с
частично заполненными верхними оболочками проявляют хим. активность. Если
электронов на внешней оболочке одинаково, то их свойства похожи.
, чтобы
перейти в другую электронную оболочку. Атомы с полностью заполненной внешней
оболочкой наиболее устойчивы. Они, как правило, в хим. реакции( без спец.
условий ) не вступают. Такими системами являются атомы инертных газов. Атомы с
частично заполненными верхними оболочками проявляют хим. активность. Если
электронов на внешней оболочке одинаково, то их свойства похожи.
Примеры:
H- (порядковый
номер-1)электрон атома находится в ![]() состоянии( n=1
состоянии( n=1 ![]() =0
), т.е. один электрон в состоянии.
=0
), т.е. один электрон в состоянии.
He-
(2) электронная конфигурация ![]() . В атоме 2 электрона.
Принцип Паули допускает их размещение в 1s состоянии
при условии, спины будут противоположно направлены. Самая нижняя энергетическая
оболочка с n=1 оказывается полностью заполненной.
Более высокие энергетические уровни n>1 лежат выше и
определяют возбужденные состояния атома.
. В атоме 2 электрона.
Принцип Паули допускает их размещение в 1s состоянии
при условии, спины будут противоположно направлены. Самая нижняя энергетическая
оболочка с n=1 оказывается полностью заполненной.
Более высокие энергетические уровни n>1 лежат выше и
определяют возбужденные состояния атома.
B-(5). В атоме бора 5 электронов. Начиная с бора, происходит
заполнение p-состояний во 2-ой оболочке. Говорят, что
заполняется p- подоболочка при n=2.
Электронная конфигурация ![]() . Энергия 2p-состояния лежит выше, чем энергия 2s-состояния(
вследствие большего значения
. Энергия 2p-состояния лежит выше, чем энергия 2s-состояния(
вследствие большего значения ![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.