Если
силовое поле, в котором движется описываемая частица, стационарно, то потенциал
его не зависит явно от времени, а функция ![]() имеет
смысл потенциальной энергии и зависит только от координат
имеет
смысл потенциальной энергии и зависит только от координат ![]() . В этом случае волновую функцию можно
представить как произведение двух. Одна функция зависит только от
. В этом случае волновую функцию можно
представить как произведение двух. Одна функция зависит только от ![]() , другая – только от времени
, другая – только от времени ![]() :
:
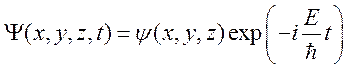
Подставим последнее выражение в уравнение Шрёдингера
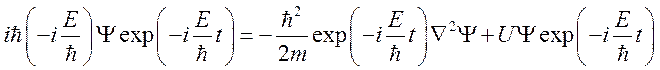 .
.
После
сокращения на временной множитель 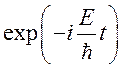 и некоторых
элементарных преобразований получим:
и некоторых
элементарных преобразований получим: 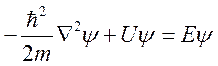 (*).
(*).
Это
уравнение Шрёдингера для стационарных состояний. В него входит только
координатная часть волновой ф-ции –![]() . Если последняя будет
найдена, то полная волновая ф-ция находится домножением координатной части на
временной множитель
. Если последняя будет
найдена, то полная волновая ф-ция находится домножением координатной части на
временной множитель 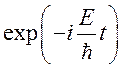 .
.
Поскольку вероятность определяется квадратом волновой ф-ции, а квадрат комплексной величины находится умножением на комплексно сопряженную, то имеет место следующее соотношение для стационарных волновых функций:
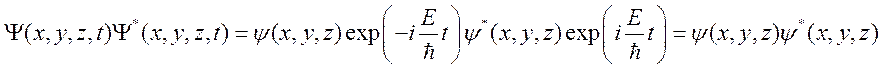 .
.
Таким
образом, чтобы найти волновую ф-цию для стационарных состояний, необходимо
решить уравнение (*) и знать полную энергию ![]() .
.
Свободное движение частиц.
Во
время свободного движения квантовой частицы никакие силы на нее не действуют и
можно ее потенциальную энергию равной нулю. Пусть движение частицы происходит в
направлении ![]() , тогда (*) принимает вид:
, тогда (*) принимает вид: 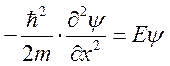 .
.
Частным
решением этого уравнения является ф-ции вида ![]() , где
, где ![]() и
и ![]() –
константы. Если подставить искомое решение в само уравнение, то мы получим
связь энергии частицы
–
константы. Если подставить искомое решение в само уравнение, то мы получим
связь энергии частицы ![]() и величины
и величины ![]() :
: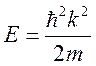
Полная
волновая функция с учетом зависимости от времени для свободной частицы имеет
вид ![]() . Это плоская монохроматическая волна с
частотой
. Это плоская монохроматическая волна с
частотой ![]() и волновым числом
и волновым числом ![]() .
Так как
.
Так как 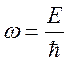 , а
, а 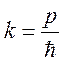 , то
, то 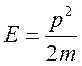 .
.
Мы
получили обычное выражение, связывающее кинетическую энергию и импульс
нерелятивистской частицы. Величины ![]() и
и ![]() такой частицы ничем не ограничены, те
свободная квантовая частица может иметь любое значение энергии и импульса.
Вероятность обнаружения частицы в интервале координат
такой частицы ничем не ограничены, те
свободная квантовая частица может иметь любое значение энергии и импульса.
Вероятность обнаружения частицы в интервале координат ![]() определяется
соотношением
определяется
соотношением ![]() .
.
Величину,
стоящую перед ![]() , будем называть плотностью
вероятности
, будем называть плотностью
вероятности ![]() .
.
Это означает равную вероятность обнаружения
свободной частицы в любой точке направления ![]() , т.е.
область движения вдоль «
, т.е.
область движения вдоль «![]() » у свободной частицы
ничем не ограничена. Энергия частицы может быть любой, начиная с нуля, так как
из уравнения Шрёдингера нет никаких ограничений на величину
» у свободной частицы
ничем не ограничена. Энергия частицы может быть любой, начиная с нуля, так как
из уравнения Шрёдингера нет никаких ограничений на величину ![]() .
.
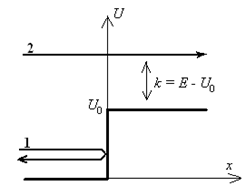
Так говорит классическая механика
Рассмотрим случай ![]() .
.
Решение ур. Шрёдингера покажет, что происходит с
реальными частицами. С учетом того, что в первой области ![]() , а во второй
, а во второй ![]() , ур.
Шредингера для них будет выглядеть так:
, ур.
Шредингера для них будет выглядеть так:
Первая область: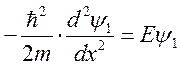 ,
Вторая область:
,
Вторая область: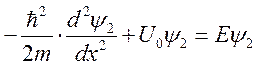
Решения этих уравнений имеет вид
![]()
![]() .
. 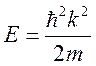
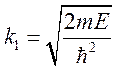
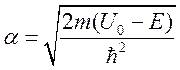
Первое слагаемое в ![]() описывает
падающую волну, второе – отраженную от потенциальной ступеньки. Так как есть
решение уравнения и во второй области, то для квантовой частицы имеется
конечная вероятность попадания во вторую область. Эта вероятность определяется
величиной
описывает
падающую волну, второе – отраженную от потенциальной ступеньки. Так как есть
решение уравнения и во второй области, то для квантовой частицы имеется
конечная вероятность попадания во вторую область. Эта вероятность определяется
величиной ![]() . Очевидно, что второе слагаемое
. Очевидно, что второе слагаемое ![]() , растущее с увеличением
, растущее с увеличением ![]() , должно равняться нулю. Поэтому
, должно равняться нулю. Поэтому![]() . Остается первое слагаемое, квадрат
которого и определяет конечную вероятность обнаружения частицы за потенциальной
ступенькой. Эта вероятность экспоненциально падает с увеличением
. Остается первое слагаемое, квадрат
которого и определяет конечную вероятность обнаружения частицы за потенциальной
ступенькой. Эта вероятность экспоненциально падает с увеличением ![]() .
.
В точке ![]() должно выполняться
условие непрерывности
должно выполняться
условие непрерывности ![]() и
и ![]() , т.е.
, т.е. ![]() и
и 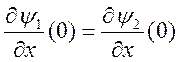 .Отсюда
получаются формулы, связывающие коэффициенты
.Отсюда
получаются формулы, связывающие коэффициенты ![]() :
:
![]() .
.
Таким образом 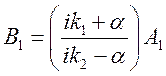 ;
; 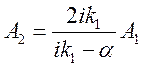
Окончательно волновые функции для первой и второй областей имеют вид:
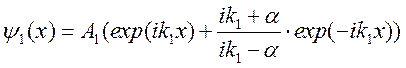
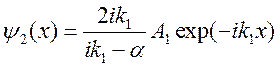
Зайдя во вторую область частица ОБЯЗАТЕЛЬНО вернется.
Перейдем
к рассмотрению случая, когда энергия частицы больше высоты ступеньки (![]() ).
).
Ур.
Шрёдингера для первой и второй областей выглядит также. С учетом того, что ![]() , решения для этих областей теперь имеют
вид
, решения для этих областей теперь имеют
вид
![]()
![]() , где
, где 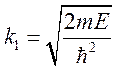 ,
, 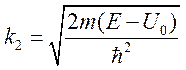 .
.
Оба
решения представляют собой суммы падающей и отраженной волн. Так как во второй
области нет отраженной волны, то ![]() . Для нахождения связи
коэффициентов
. Для нахождения связи
коэффициентов ![]() воспользуемся снова
условиями непрерывности функции
воспользуемся снова
условиями непрерывности функции ![]() и ее первой производной
в точке
и ее первой производной
в точке ![]() . Первое условие дает
. Первое условие дает ![]() , из второго условия следует
, из второго условия следует ![]() , из этих уравнений находим
, из этих уравнений находим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.