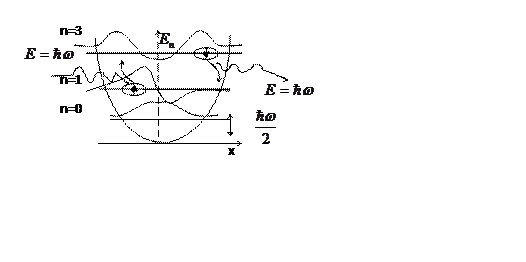
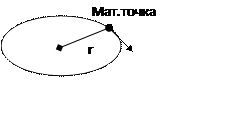
В
классической механике для материальной точки момент импульса определяется как
векторное произведение радиуса-вектора точки на ее импульс: 
.
1.
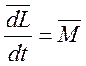
2.
, если система изолированная или движется в
центрально симметричном поле.
В квантовой механике момент импульса используется при описании движения частиц в центрально-симметричных полях. Рассмотрим простейший пример:
отрицательно заряженный
электрон движется в поле положительно заряженного протона.
Для микрочастиц можно ввести две разновидности момента импульса :
1. Орбитальный .
2. Собственный
(спин - 
)
|
, 
, S-спин
(постоянная величина).
Орбитальный и собственный моменты импульсов являются квантованными.
Квантование орбитального момента.
Орбитальное
движение – двумерное движение. Величина орбитального момента частицы
определяется: 
где l=
0, 1, 2, 3,…Таким образом, если l=0,
то
L=0, а если l=1,
то
L=
.
Величина
проекции орбитального момента на некоторое выделенное направление Z
в пространстве: 
, где 
(всего
2l+1 значений), а l
– орбитальное
квантовое число. Каждая проекция от соседней проекции отличается на 
.
Итак, как величина, так и направление квантово-механического орбитального момента могут меняться лишь дискретным образом. Орбитальный момент оказывается квантованным.
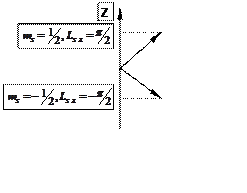Наряду с орбитальным
моментом частицы могут иметь свой собственный момент импульса, не связанный с
их пространственным перемещением. Величина собственного момента характеризуется
спиновым квантовым числом S
и связана с ним соотношением: 
. Проекция спина 
на выделенное направление имеет лишь
дискретные значения: 
, где 
- магнитное спиновое квантовое число.
Для
электронов 
может быть только две возможные ориентации
, соответствующие =
, а =
.
=
-
«спин - вверх», а =
- «спин
- вниз».
35. Атом водорода. Квантование состояний. Спектральные переходы.
Атом водорода, состоящий из двух взаимодействующих частиц, представляет собой наиболее простую квантово-механическую систему для применения теории Шредингера. Использование последней дало первые успешные результаты квантовой механики в области описания атомов.
В состав атома водорода входят положительно заряженное
ядро-протон и отрицательно заряженный электрон. Мы будем использовать
упрощенный подход, в котором взаимодействие этих частиц считается чисто
электростатическим. В этом случае уравнение Шредингера имеет точное
аналитическое решение.
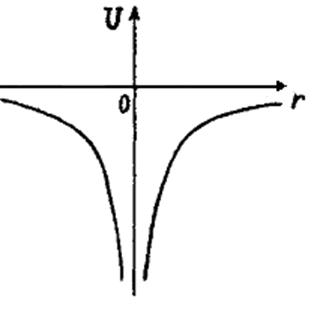
На рис. изображён график зависимости от расстояния энергии кулоновского взаимодействия электрона и протона:
Как следует из графика, электрон находится в своеобразной трёхмерной потенциальной яме.
Состояния электрона в этом случае являются связанными и должны характеризоваться набором четырёх квантовых чисел. Три из них определяются тремя пространственными ограничениями движения электрона, а четвертое – наличием у него собственного момента – спина. Различным наборам этих квантовых чисел должны соответствовать различные собственные функции уравнения Шредингера, имеющие форму стоячих волн, а также различные значения полной энергии и момента импульса электрона.
Таким образом, задача описания состояния атома водорода сводится к нахождению квантовых чисел, собственных волновых функций, значений энергии и момента импульса электрона.
Волновые функции и квантовые состояния атома водорода
Поскольку масса протона значительно превышает массу электрона (mp ≈ 1836me), задачу квантово-механического описания атома водорода можно свести к описанию движения электрона в поле неподвижного протона. Стационарное уравнение Шредингера для волновой функции электрона в этом случае записывается следующим образом:
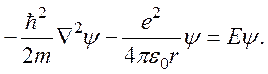
Так как система обладает центральной симметрией, удобно
перейти к сферическим координатам, характеризуя положение электрона по
отношению к ядру радиусом вектором 
, полярным углом θ и азимутальным углом φ (см.
рис.).
В этих координатах уравнение Шредингера принимает вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.