Физика \ Физика

Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 5

Звуковые или акустические волны - распространяющиесяв упругой среде слабые возмущения – механические колебания с малыми амплитудами.

Волновое уравнение.

Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции Y, описывающей плоскую волну.

Y=Acos(wt-kx)

                   

                                                               

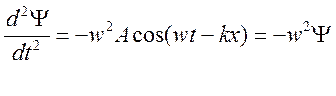
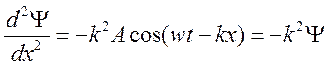
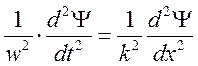
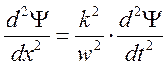
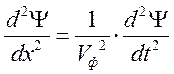      àодномерное волновое уравнение.

Решением этого уравнения  являются функции вида:   Y=Acos(wt-kx), т.к. решение линейное, то линейные комбинации такой функции – тоже  являются решением. Эти функции описывают распространение возмущений в пространстве.

В общем случае, когда нужно учесть три пространственных измерений, уравнение имеет вид:

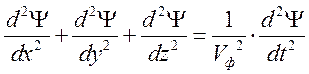
Если есть система, распределенная в пространстве, её собственная динамика описывается таким уравнением, то в такой системе могут распространяться волны. Коэффициент стоящий в правой части уравнения характеризует квадрат фазовой скорости. 

Плоские гармонические волны и их характеристики.

Фронт волны – плоскость, перпендикулярная направлению распространения волны.

 


                                                                                    Пусть колебания листа происходят по закону косинуса.                                    Смещение от положения равновесия  Y=Acos(wt).

Вызовем плоскость, которая соответствует волновому фронту, на

расстоянии х от листа.

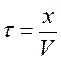                t – время запаздывания колебаний,  V- скорость распространения волны.

Y=Acos(w(t-t )).  Пусть потери энергии нет Þ амплитуда и частота будут точно такие.

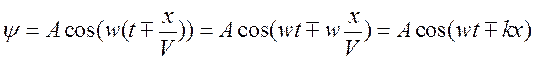,  где k- волновое число  и  .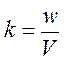

 – уравнение плоской волны.

 радиус вектор в любой точке волновой поверхности,

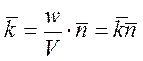    – волновой вектор.

Y=Acos(wt-kx),   где

·  j=wt-kx – фаза зависит от t и x.

·  Y - смещение

·  А – амплитуда

·   w – циклическая частота. 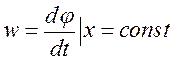 Показывает быстроту изменения фазы   колебаний в определенной точке пространства. w=[c-1]

·  n - частота

·  T –период

·    к- волновое число. 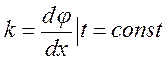    Показывает быстроту изменения фазы колебаний в пространстве в фиксированный момент времени.

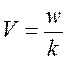·   - скорость волнового процесса.  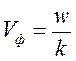  –фазовая скорость волны.

·  l- длина волны.    k* l=2p          wT=2p

l- аналог Т, пространственный период волнового процесса.

                                          l= VфT

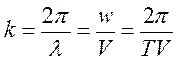
Уравнение волны можно представить в комплексном виде: Y=Аеi(wt-kx).

В общем случае jо!=0 , тогда   Y=Acos(wt-kx+ jо), à   Y=Аeij еi(wt-kx).

11.Волновое уравнение для поперечных упругих волн на непрерывной струне. Фазовая и групповая скорости волн на струне.

Волновое уравнение для поперечных волн на струне.

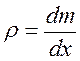
1.  упругость (возвращающее воздействие)

2.  инертность

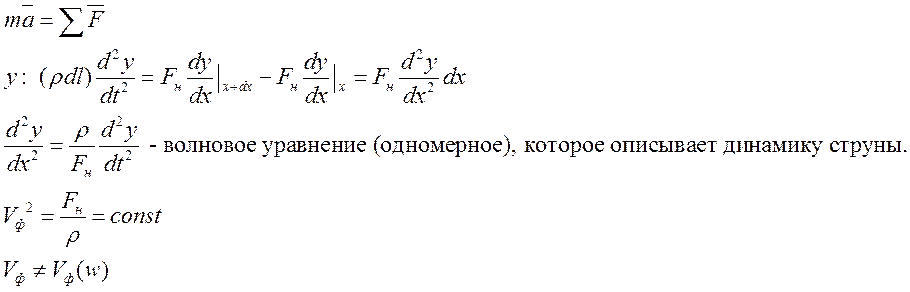
Поперечные волны на непрерывной однородной струне имеют дисперсии.

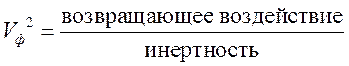
12.Импеданс (волновое сопротивление) непрерывной струны. Волны на границе раздела.

Возникает поперечная гармоническая волна:

  1.  - быстрота перемещения постоянной фазы.
  2.  - движение группы волн (энергии).
  3.  - амплитуда колебаний скорости частиц

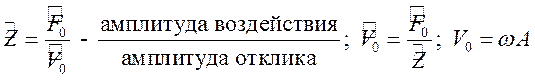
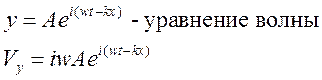
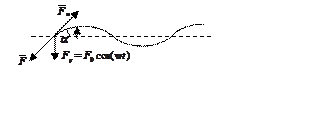Внешнее воздействие можно связать с поперечной составляющей силы натяжения.

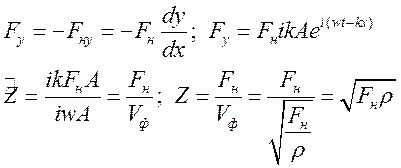
 - импеданс

Два колебания в одной и той же фазе, т.к. величина действительная

Источник все время совершает работу. Источником это воспринимается, как потеря энергии (поэтому )

, , ;


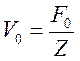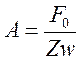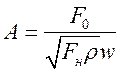
20. Поперечные волны на границе раздела струн. Стоячие волны на струне.

Поперечные волны на границе раздела двух струн.

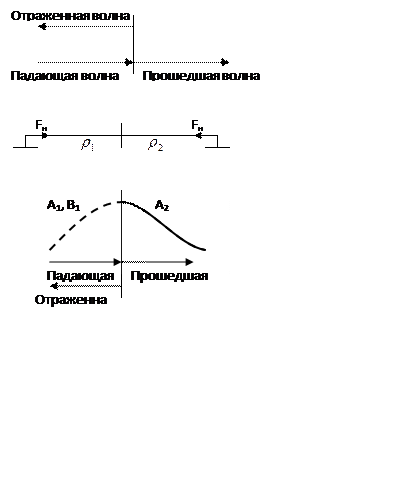
На границе раздела двух сред волны отражаются и преломляются.

:

1. 

2. 

    (1)

   (2)

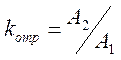    -  коэффициент прошедшей волны.

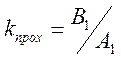   -  коэффициент отраженной волны.

Домножим (1) на kи вычтем из (1) (2)

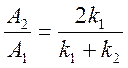   (3)

Домножим (1) на kи прибавим (1) к (2)

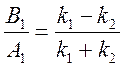
домножим 3 на  =>

   =>

   => 

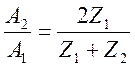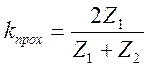
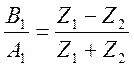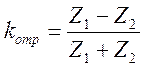
1)            => 

Скачать файл