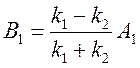 ,
, 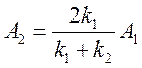 .
.
Мы
получили, что коэффициент ![]() , определяющий амплитуду
отраженной волны, отличен от нуля. Это означает, что при
, определяющий амплитуду
отраженной волны, отличен от нуля. Это означает, что при ![]() имеется конечная вероятность отражения
частиц от барьера. Это чисто квантово-механический эффект, связанный с
проявлением волновых свойств частиц.
имеется конечная вероятность отражения
частиц от барьера. Это чисто квантово-механический эффект, связанный с
проявлением волновых свойств частиц.
Определим
для потенциальной ступеньки коэффициенты отражения R и прохождения Т.
Пусть на ступеньку из первой области падает пучок частиц. Скорость частиц в
первой области ![]() связана с их импульсом:
связана с их импульсом: 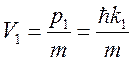 .
Частицы, прошедшие во вторую область, будут иметь скорость
.
Частицы, прошедшие во вторую область, будут иметь скорость 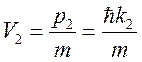 .
Итак, имеется 3 потока: падающих частиц интенсивностью
.
Итак, имеется 3 потока: падающих частиц интенсивностью ![]() ,
отраженных частиц интенсивностью
,
отраженных частиц интенсивностью ![]() и прошедших
интенсивностью
и прошедших
интенсивностью ![]()
Коэффициент
отражения определим как отношение интенсивностей отраженного и падающего
потоков: 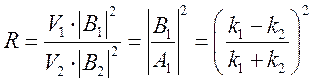 .
.
Коэффициент
прохождения – как отношения интенсивностей прошедшего и падающего потоков: 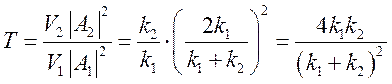
Складывая
выражения для R и Т, получаем ![]() . Данное равенство означает, что частица
либо отражается от ступеньки, либо проходит во вторую часть. Если рассматривать
не поток, а отдельно взятые частицы, то R – средняя вероятность отражения
частиц от потенциальной ступеньки, а Т – средняя вероятность
прохождения. Если частицы с
. Данное равенство означает, что частица
либо отражается от ступеньки, либо проходит во вторую часть. Если рассматривать
не поток, а отдельно взятые частицы, то R – средняя вероятность отражения
частиц от потенциальной ступеньки, а Т – средняя вероятность
прохождения. Если частицы с ![]() движутся к ступеньке не
->, а <-, то также имеет место отражение. Причем R остается прежним, если
движутся к ступеньке не
->, а <-, то также имеет место отражение. Причем R остается прежним, если ![]() и
и ![]() не менять. Для квантовых частиц
любое резкое изменение
не менять. Для квантовых частиц
любое резкое изменение ![]() всегда приводит к определенному
отражению от этой области.
всегда приводит к определенному
отражению от этой области.
Туннельный эффект.
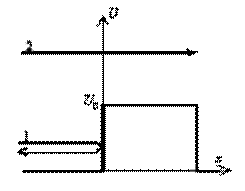 Проанализируем теперь движение квантовой частицы.
Пусть
Проанализируем теперь движение квантовой частицы.
Пусть ![]() , тогда 1 – область слева от барьера, 2 -
область барьера, 3 - область справа от барьера. Волновые функции частицы в этих
областях обозначим соответственно
, тогда 1 – область слева от барьера, 2 -
область барьера, 3 - область справа от барьера. Волновые функции частицы в этих
областях обозначим соответственно![]() . Запишем уравнение
Шрёдингера для каждой области:
. Запишем уравнение
Шрёдингера для каждой области:
Первая
область 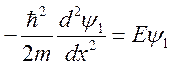
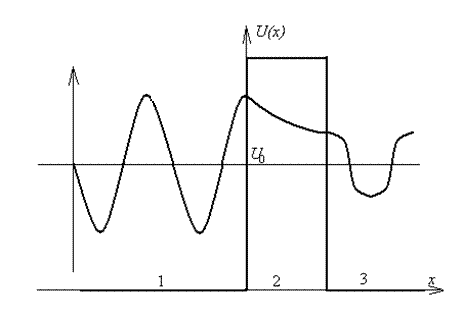 Вторая область
Вторая область 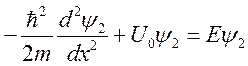
Третья
область 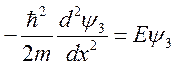
Решения
этих уравнений имеют вид (очевидно ![]() и
и![]() )
)
![]()
![]()
![]()
Так
как в первой области решение содержит отраженную волну, то это означает, что
частица имеет конечную вероятность отражения от барьера (у классической частицы
вероятность равна 1). Так как в третьей области есть прошедшая волна, то у
частицы есть вероятность прохождения за барьер (с классической точки зрения в
принципе не может быть). Такая способность квантовых частиц проникать сквозь
потенциальный барьер при ![]() получила название
туннельный эффект.
получила название
туннельный эффект.
Коэффициенты
![]() связаны между собой Эта связь может быть
определена из условий непрерывности
связаны между собой Эта связь может быть
определена из условий непрерывности ![]() и
и ![]() на границах барьера:
на границах барьера: ![]()
![]() ,
, ![]() ,
, 
Для описания туннельного эффекта используются не сами коэффициенты, а их отношения. Вероятность отражения частицы от потенциального барьера – коэффициент отражения R и вероятность прохождения частицы сквозь барьер – коэффициент прозрачности барьера D.
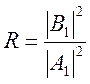 ,
, 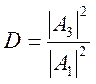
Оба коэффициента связаны соотношением![]() .
.

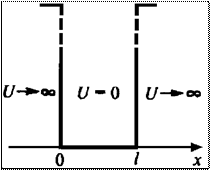 Потенциальная яма
Потенциальная яма
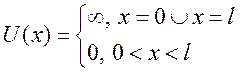 , где
, где ![]() -
ширина ямы, а энергия отсчитывается от ее дна. Никакая частица не может выйти
из этой ямы. Если частица классическая, то, в зависимости от скорости,
если
-
ширина ямы, а энергия отсчитывается от ее дна. Никакая частица не может выйти
из этой ямы. Если частица классическая, то, в зависимости от скорости,
если
1) ![]() , то
положим равной 0; 2)
, то
положим равной 0; 2)![]() : частица движется между
стенками, и график плотности распределения вероятности будет выглядеть в виде
прямой (см. рисунок).
: частица движется между
стенками, и график плотности распределения вероятности будет выглядеть в виде
прямой (см. рисунок).
Для
реальной частицы: запишем уравнение Шредингера: 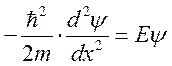 .
.
За
пределы ямы частица не проникает, поэтому волновая функция вне ямы равна 0,
следовательно, на границах ямы ![]() . Решение ищем в виде
. Решение ищем в виде ![]() .
. ![]() .
. ![]() . По второму граничному условию:
. По второму граничному условию: ![]() .
. 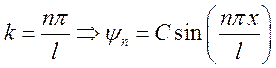 , где n - квантовое число.
, где n - квантовое число.
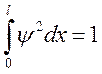 , т. к. вероятность обнаружения частицы
внутри ямы равна 1, следовательно
, т. к. вероятность обнаружения частицы
внутри ямы равна 1, следовательно 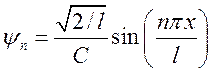 . Решения найдены в
виде стоячих волн.
. Решения найдены в
виде стоячих волн.
Рассмотрим
Е: 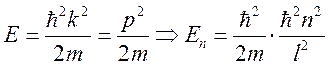 , где
, где ![]() , т. е.
есть множество значений энергии, которые частица не принимает. Таким образом,
энергия дискретна, т. е. квантована. Чем меньше
, т. е.
есть множество значений энергии, которые частица не принимает. Таким образом,
энергия дискретна, т. е. квантована. Чем меньше ![]() , тем
выше
, тем
выше ![]() ; состояния частицы дискретны. Энергия
пробегает ряд значений, не равных 0. Разрешенные энергии частицы называются
энергетическими уровнями, они появляются, если частица ограничена в
пространстве.
; состояния частицы дискретны. Энергия
пробегает ряд значений, не равных 0. Разрешенные энергии частицы называются
энергетическими уровнями, они появляются, если частица ограничена в
пространстве.
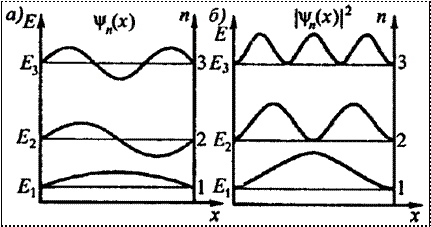
Изобразим
волновую функцию на фоне уравнений при ![]() .
.
![]() - основное состояние (основной
энергетический уровень).
- основное состояние (основной
энергетический уровень).
У классической частицы этот график выглядит в виде прямой, параллельной оси Ох.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.