Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 7

В среде будут распространяться электромагнитные волны, в них будут присутствовать . Волна носит электромагнитную природу.

Плоские электромагнитные волны и их структура.

 - описывает возмущение магнитной составляющей вблизи плоскости. Возмущение будет распространятся в пространстве с

           

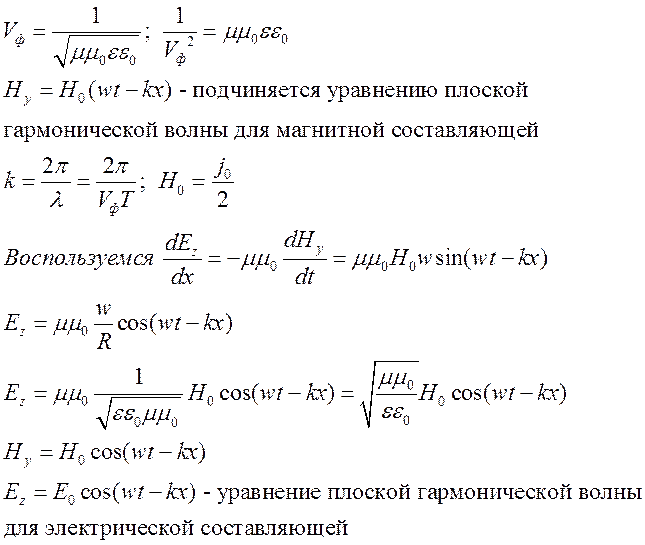
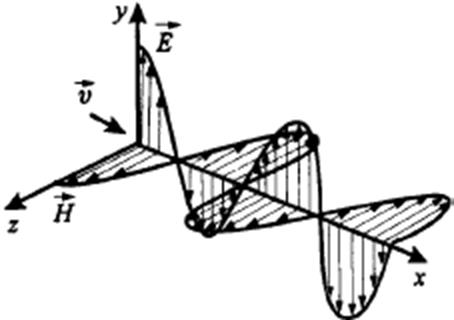
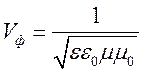 Фазы у  и  одинаковые.

В вакууме  и, тогда,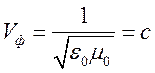

16.Энергия электромагнитной волны. Вектор Пойнтинга.

электромагнитных волн

Если знаем направление вектора E и вектора H, то мы знаем направление распространения волны.

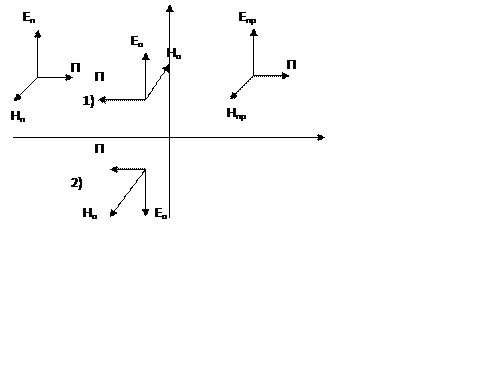
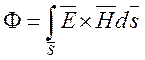
17.Импеданс среды для электромагнитных волн. Электромагнитные волны на границе раздела сред.

Импеданс среды для электомагнитных волн

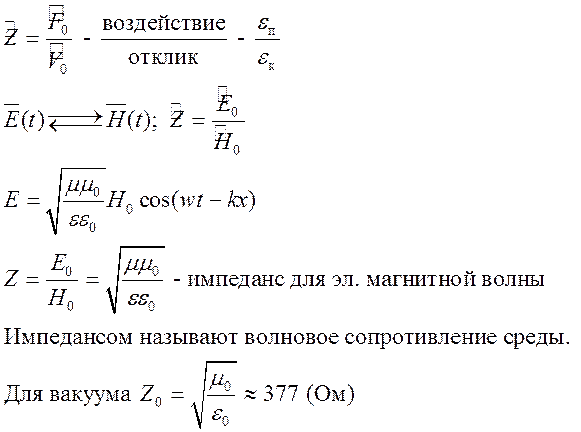
Знание импеданса позволяет полностью восстановить параметры электромагнитной волны, если известны характер источника и среды.

Условия на границе раздела двух сред.

Одна волна отраженная, другая прошедшая.

    

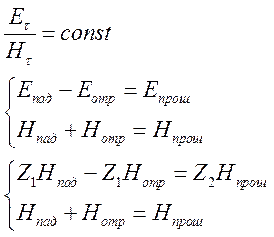
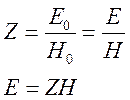
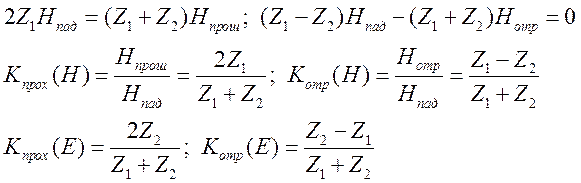
Смена знаков связана с фазовыми соотношениями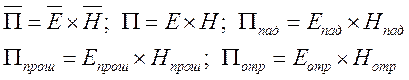

Перемножим коэф. прохождения, получим количество прошедшей энергии от падающей волны на поверхность: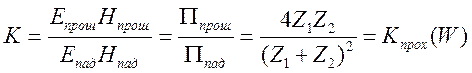

перемножим коэф. отражения и получим количество отраженной энергии: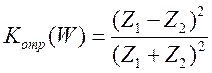

Если  то энергия не будет отражаться.

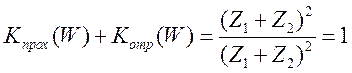 - следствие закона сохранения энергии.

Коэф. выражаются через коэф. преломления среды:

   

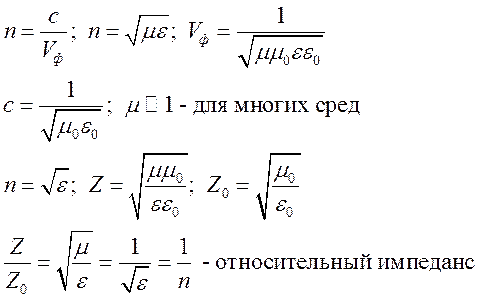
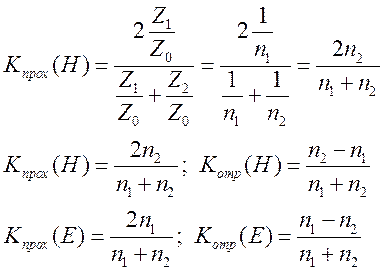
Оптически более плотная среда – это среда с большим коэффициентом преломления.

1.  - нет отражения

2.  - первая среда плотнее второй

     - H в противофазе,      - E в фазе

3.  - вторая среда плотнее первой

     - H в фазе

     - E в противофазе

18.Стоячие электромагнитные волны.

Энергия, переносимая волной. Стоячие волны.

При изучении механических колебаний было установлено, что полная энергия колебаний гармонического осциллятора W = mω²A²/2 , где А — амплитуда колебания, (см. формулу (3.14)). Именно эта энергия переносится волной посредством возбуждения колебаний близлежащих частиц. Более полной характе­ристикой процесса переноса энергии волной является вектор плотности потока энергии волны j , который определяет количество энергии, переносимое волной через единицу площади в одну секунду в направлении ее распространения. Если v – скорость волны, то за время Dt через площадку DS, перпендикулярную направлению распространения, переносится количество энергии:

,                                      

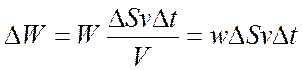где w — плотность энергии, заключенной в объеме V.

Разделив это выражение на DSDt, получим величину плотности потока энергии:

j = w×v.                                                             (3.58)

Наконец, если ввести вектор , равный по величине фазовой скорости волны и направленный вдоль волнового вектора  (3.55), получим выражение для вектора плотности потока энергии:

.                                                            (3.59)

Следовательно, направление вектора плотности потока энергии совпадает с направлением распространения волны.

Вектор (3.59) называется вектором Умова-Пойнтинга. Он является важной характеристикой переноса энергии волной я сохраняет свое значение и в тех случаях, когда речь идет не только о колебаниях частиц, но и о волновом процессе изменения любых физических величин, например температуры, электрического или магнитного полей.

Необычное перераспределение энергии колебаний происходит при наложении двух волн, бегущих навстречу друг другу, в том случае, когда разность фаз между волнами в процессе распространения волн остается постоянной. Такая ситуация реализуется при отражении бегущей волны от препятствия, например, при возбуждении упругой волны в струне, один из концов которой закреплен. При этом возникает отраженная волна, бегущая навстречу первой. Пусть для простоты начальные фазы обеих волн равны нулю. Тогда результирующая волна будет суммой двух волн, бегущих в противоположных направлениях:

u₁ = u₀ cos(ωt – kx),  u₀ = u₀ cos(ωt + kx).                 (3.60)

Сложив эти уравнения и преобразовав результат сложения по формуле для суммы косинусов, получим:

u = u₁ + u₀ = 2u₀cos kx×cos ωt.                                   (3.61)