Параметры термодинамического равновесия, внутренняя энергия, число частиц и объем неполностью определяют равновесное состояние макросистем. Любая макросистема подвергается еще механическому воздействию со стороны других макросистем. Мерой механического взаимодействия является давление. Для того, чтобы понять механизм давления с точки зрения квантовой механики, рассмотрим идеальный газ, заключенный в прямоугольный объем с размерами lx, ly, lz рис. Пусть стенка с координатой x будет подвижной (поршень). В выбранной системе координат размер объема lx будет совпадать с координатой x. Энергия i-й орбитали будет определяться соотношением
ε = 
= 
(
)
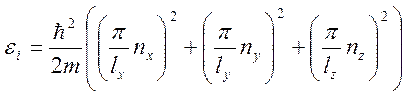, где nx, ny, nz - целые числа (2)
Предположим, что эта орбиталь
заполнена и переместим поршень на расстояние dx. Как
видно из формулы (2), увеличение размера 
приводит
к уменьшению энергии состояния. Вычислим это уменьшение. Заменяя на x, получаем
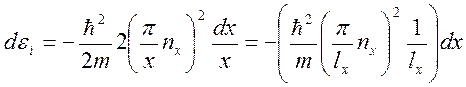(3)
Выражение в фигурных
скобках совпадает по размерности с силой. Введем обозначение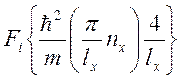 
и перепишем (3): 
.
ассматривая 
как силу, с которой частица, заполняющая i-ю орбиталь, взаимодействует со стенкой, видно, что
уменьшение энергии 
происходит за счет работы этой
силы по перемещению поршня на расстояние dx.
Обратимся теперь к системе в целом и построим ансамбль, представленный эквивалентными системами во всех доступных состояниях. Переместим поршень так, чтобы частицы при этом не меняли свои орбитали. Это означает, что число доступных состояний не меняется. Иначе говоря, процесс осуществляется при постоянной энтропии.
Рассмотрим одну из систем ансамбля. Для нее внутренняя энергия:
,
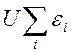где суммирование ведется по заполненным орбиталям. Тогда
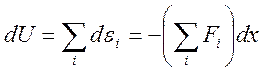
Преобразуем последнее выражение, введя изменение объема 
,
,
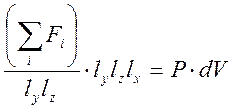где символом P обозначено давление, которое оказывают частицы системы на поршень.
Усредняя по ансамблю, получаем 
Перепишем с учетом того, что процесс производится при постоянной энтропии и постоянном числе частиц:
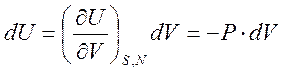
Из этой формулы следует определение давления:
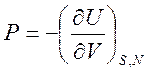
Последняя формула не всегда бывает удобна для использования. Поэтому, рассматривая, как и прежде, процесс при постоянной энтропии, получим еще одно выражение для давления.
При постоянном числе частиц энтропия является только функцией энергии и объема
S = S(U,V). Полный дифференциал
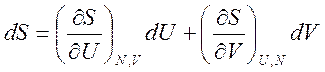в нашем случае dS = 0,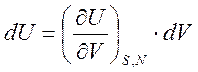 
В результате получаем формулу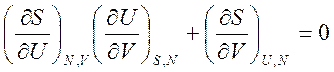 
Учитывая, что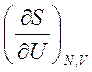 
=
и
определение давления получаем
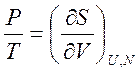
Это определение более удобное и учитывает изменение энтропии при изменении объема.
47.Основное термодинамическое тождество.
Как было отмечено ранее, энтропия является функцией числа частиц, объёма и энергии S=S( U, V, N ). Вычислим полный дифференциал:
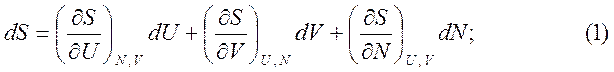
Учитывая, что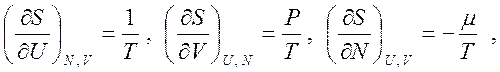 
получаем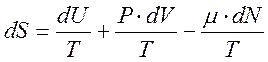 
или 
Формула (2) носит название «термодинамического тождества», которое в форме, более удобной для анализа имеет вид:
Все величины, входящие в (3), имеют размерность энергии. Величина TdS имеет особый смысл, она обозначается символом dQ и называется количеством тепла:
Это энергия, которая передаётся системе в виде хаотического движения частиц, увеличивая при этом число доступных состояний. Формула (3) представляет собой закон сохранения энергии и известна в термодинамике как первое начало. Это означает, что внутренняя энергия dU возрастает при добавлении тепла dQ, убывает за счёт работы системы над внешними телами PdV, увеличивается при добавлении частиц в систему μdN. Величина μdN называется химической работой.
Термодинамическое тождество позволяет определить новый физический смысл химического потенциала: химический потенциал численно равен работе, необходимой для того, чтобы добавить частицу в систему.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.