Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 35

Последняя формула чаще всего используется для вычисления среднего числа частиц в системе. Среднее значение энергии системы

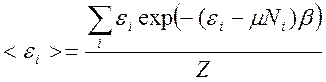
44.Распределение Ферми-Дирака.

Обратимся теперь к системе частиц с полуцелым спином. Такие частицы (фермионы) подчиняются принципу Паули и орбиталь может быть заполнена только одной частицей или быть незаполненной. Большая статистическая сумма для такой системы очень проста:

Среднее число фермионов на орбитали:

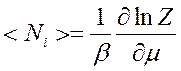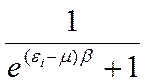=                          (1)

Функция (1) называется распределением Ферми-Дирака и в принятых обозначениях имеет вид:

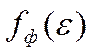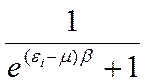=                 (2)

Распределение Ферми-Дирака имеет смысл среднего числа фермионов на орбитали. Однако значения функции Ферми-Дирака лежит в пределах от 0 до 1 и в отличие от распределения Бозе-Энштейна можно говорить о том, что функция (2) может быть истолкована как вероятность заполнения орбитали с энергией ε. При абсолютном 0 все орбитали вплоть до химического потенциала заполнены, а орбитали с энергиями  остаются незаполненными. С ростом температуры значения <1 во всем интервале энергий.

45.Распределение Бозе-Эйнштейна.

Рассмотрим систему частиц с целым спином, которые принято называть бозонами. Такие частицы не подчиняются принципу Паули и могут быть даже все в состояниях, и описываемых одной и той же волновой функцией. Т.е. такие частицы могут все заполнить одну орбиталь. Так, если поместить систему бозонов в термостат, то при любом способе заполнения орбитали обеспечивается условие применимости большого канонического распределения для системы, которая представляет собой орбиталь. Обозначим ξ _i энергию частицы, если она заполняет орбиталь. Если в квантовом состоянии j=2,число частиц на орбитали равно 2,а энергия частиц ε₂ = 2 ξ _i  . Составим большую статистическую сумму

                         (1)

Учитывая, что N очень большое число, то верхний предел в сумме (1) заменим на бесконечность.

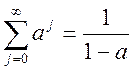, если а<1. В случае, когда a>1 – такая сумма расходится.

Величина  должна быть меньше единицы при любых значениях энергии ε_i   в том числе, когда ε_i =0. Для выполнения этого условия необходимо, чтобы химический потенциал был бы отрицателен (μ<0). При выполнении этих условий

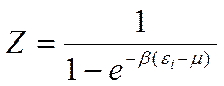            Z-большая статическая сумма.    

Вычислим среднее число бозонов на орбитали, пользуясь (1)

     

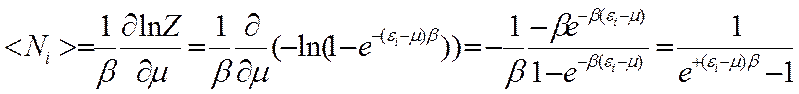
Полученный результат носит название распределения Бозе-Энштейна.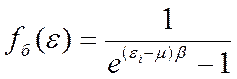                  - среднее число бозонов на орбитали с энергией e.

Квазиклассическое распределение.

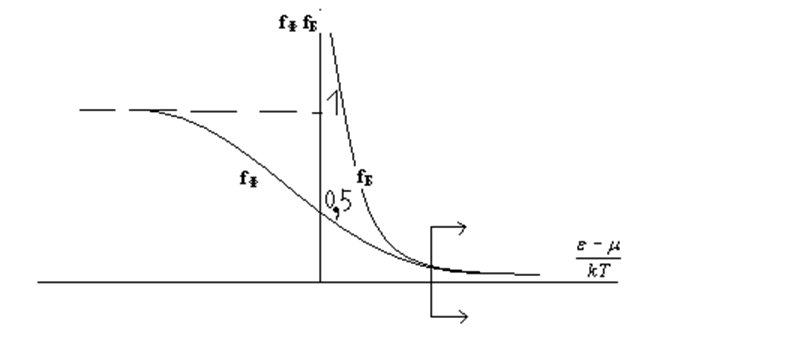
На рисунке 1 представлены графики функций Ферми-Дирака и Бозе-Эйнштейна, которые могут быть представлены общей записью

(1) 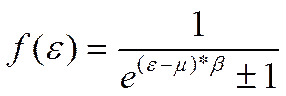           , где знак (+) соответствует распределению Ферми-Дирака, а знак (-)- распределению Бозе-Эйнштейна. Различие между распределениями исчезает, если в формуле (1) можно пренебречь 1. Это возможно, когда во всем интервале энергий будет выполняться условие:    >>1             (2)

При b>0 условие (2) будет выполняться, если химический потенциал будет отрицательным (m<0).

При выполнении условия (2) квантовые распределения (1) переходят в квазиклассическое распределение      

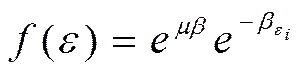 ,                                                                            (3)

которое одинаково приемлемо и для бозонов и для фермионов. Физический смысл функции (3) вытекает из смысла функций (1), с одной стороны, это среднее число частиц на орбитали, с другой- это вероятность заполнения орбитали.

Квантовые распределения (1) и квазиклассическое распределение весьма удобны для анализа тех систем, для которых квантовая механика позволяет определить полное число

частиц системы

                                               

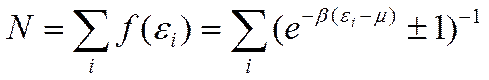
                                                 (4)
        и внутреннюю энергию системы

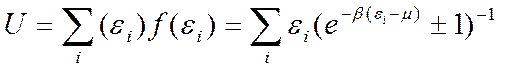 .                                                 (5)

При известных величинах N и U формулы (4) и (5) позволяют определить параметры термодинамического равновесия системы – температуру и химический потенциал

46.Давление системы частиц.