Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 19

Магнитное спиновое квантовое число m_s определяет величину проекции собственного механического момента электрона на выделенное направление z:

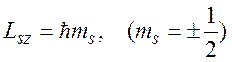
Из вышесказанного видно, что любой энергетический уровень имеет 2n² – кратное вырождение. Одной и той же энергии состояния при этом соответствует 2n² возможных волновых функций с разными значениями  (следовательно, и с разными значениями L, L_Z, L_SZ).

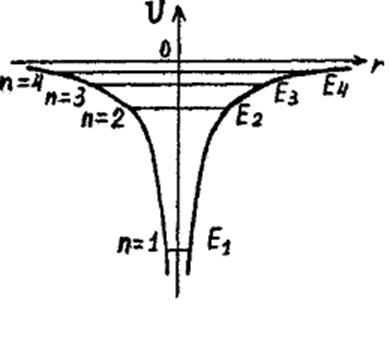
На рис. изображены четыре первых энергетических уровня атома водорода на фоне зависимости U(r). Состояние с n=1 имеет самую низкую энергию и, следовательно, является наиболее энергетически выгодным для атома. Оно называется основным состоянием. Энергия основного состояния атома водорода приблизительно равна Е1≈13.6 эВ. Величину, равную по модулю Е₁ , называют энергией ионизации атома водорода. Именно такую минимальную энергию надо затратить, чтобы атом водорода распался на две составляющие – положительный ион (в данном случае это просто протон) и отрицательный электрон. Остальные состояния с n>1 являются возбужденными состояниями атома водорода. В эти состояния электрон может переходить лишь при сообщении извне необходимой по величине энергии. Чем выше энергия состояния, тем слабее электрон связан с ядром. По мере роста n разность энергий соседних состояний становится все меньше и меньше. Сама же энергия состояния стремится к нулю при стремлении n к бесконечности.

Итак, энергия состояний электрона в атоме водорода изменяется дискретно, т.е. состояния являются квантованными. Как следует из вышесказанного, только дискретно у электрона могут изменяться орбитальный момент импульса, его проекция и проекция спина на выделенное направление.

Два квантовых числа n и l определяют две важнейшие характеристики состояния – энергию и орбитальный момент импульса электрона. В атомной физике применяются специальные обозначения состояний с различными n и l. В этом обозначении первым стоит целое число, равное значению квантового числа n, а второй – латинская буква, кодирующая величину l. Состояние с l=0 называют s -состоянием, l=1 – р-состоянием, с l=2 – d-состоянием, с l=3 – f-состоянием, затем g,h и далее по алфавиту. Так как имеется условие l≤n–1, то возможны следующие состояния:

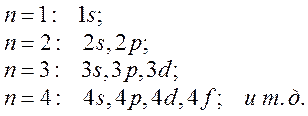
Замечание: роль радиальной плотности вероятности нахождения электрона на расстоянии r от центра ядра играет величина

Энергетические состояния и спектральные переходы атома водорода

В нормальных условиях атомы находятся в основных состояниях (для атома водорода это 1s – состояние). Если же газ, состоящий из этих атомов, нагревать, облучать светом или пучком частиц и т.д. (т.е. подвергать внешнему воздействию), то некоторые из атомов приобретают дополнительную энергию и переходят в возбужденные состояния. Оставаясь в этих состояниях незначительное время, атомы стремятся покинуть их, переходя в состояние с более низкой энергией. Эти переходы сопровождаются излучением фотонов.

Закон сохранения энергии позволяет найти возможные часто­ты излучения. Так как энергия фотона должна быть равна разности соответствующих энергетических уровней, то очевидным является равенство

где E_J – энергия верхнего уровня; E_I – энергия нижнего уровня. Фотоны являются частицами, обладающими собственным моментом импульса, поэтому при их излучении атом должен изменять свой механический момент в соответствии с законом сохранения момента импульса. Поскольку спин фотона равен единице, то орбитальное квантовое число атома при излучении фотона должно меняться на единицу

Таким образом, возможны не любые переходы атома из одного состояния в другое, а лишь подчиняющиеся последнему соотно­шению. Это соотношение называется правилом отбора. Благодаря существованию таких переходов можно наблюдать так называемые спектральные серии, хорошо известные из оптических измерений спектров излучения и поглощения атомов водорода.