Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 3

d обратно числу колебаний, в течении которых амплитуда уменьшается в e раз.
Энергия затухающих колебаний. Добротность колебательной системы.

Энергия осциллятора с трением:

E=kA²/2; A=A₀e^-bt

E=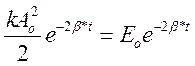

Чтобы характеризовать уменьшение энергии в системе вводится понятие добротности.

Q – добротность. Есть три определения добротности:

1.  Q=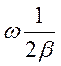

- время, за которое энергия уменьшается в e раз.

При таком определение добротность численно равна изменению фазы колебаний за время, в течении которого энергия уменьшается в e раз.

2.  b<<w_o; Q=.

3.  Пусть трение мало, найдем изменение энергии за период.

E=; ; ;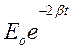

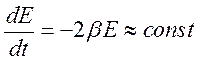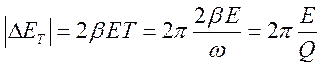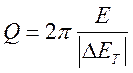
7.Вынужденные колебания осциллятора. Дифференциальное уравнение и его решение. Частота, амплитуда и фаза вынужденных колебаний.

Если на материальную точку массой , уравнение колебаний которой дано в виде , действует внешняя периодическая сила , то колебания точки будут вынужденными и уравнение ее движения примет вид , где 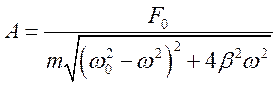, 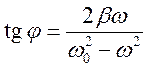. Резонанс наступает тогда, когда частота вынужденных колебаний  связана с частотой собственных колебаний  и с коэффициентом затухания  соотношением . 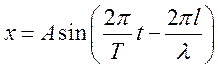При распространении незатухающих колебаний со скоростью  вдоль некоторого направления, называемого лучом, смещение любой точки, лежащей на луче и отстоящей от источника колебаний на расстояние , дается уравнением , где  - амплитуда колеблющихся точек,  - длина волны. При этом . Две точки на луче на расстояниях  и  от источника колебаний имеют разность фаз .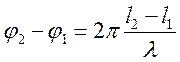

Осциллятор может находиться под внешним воздействием. Если воздействие гармоническое, то реакция осциллятора избирательна. Степень воздействия зависит от частоты воздействия.

Если частота воздействия равна собственной частоте w»w_о, то это воздействие будет максимальным, и получило название резонанса.

Дифференциальное уравнение вынужденных колебаний

1.  Пружинный маятник

F_ocos(wt) – внешнее гармоническое воздействие

; ;

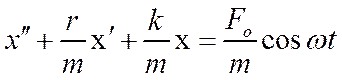
2. 

С

R

L

Колебательный контур

        E_ocoswt – гармоническое воздействие ЭДС.

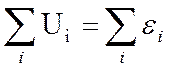; q/c+RI=-L;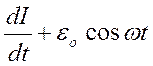

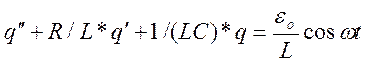
В общем случае дифференциальное уравнение вынужденных колебаний:

Дифференциальное уравнение вынужденных колебаний неоднородно. Справа не ноль. Общее решение неоднородного уравнения складывается из двух, а именно: решения общего однородного уравнения и частного решения неоднородного уравнения.

Нас интересует частного решения неоднородного уравнения, которое определяет установившееся решение.

Справа гармоническая функция, слева сумма трех функций, которые тоже должны быть гармоническими с той же частотой.

Характеристики вынужденных колебаний

x(t)=Re(x(t))

x(t)=A_oe^iwt=A_oe^ijoe^iwt

Осуществим подстановку:

x^/(t)=iwA_oe^iwt

x^//(t)=- w²A_oe^iwt

A_oe^iwt(-w²+2biw+w_o²)=f_oe^iwt

A_o=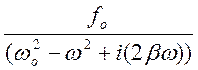

A_o=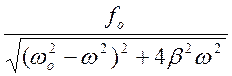; 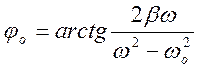. Частное решение уравнения имеет вид:

x(t)= 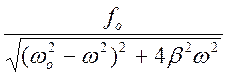cos(wt+)

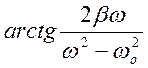Вынужденные колебания в системе оказались сдвинутыми по фазе по отношению к вынужденному воздействию.

х=Acos(wt+j_o)

1)  Частота колебаний равна частоте вынужденных колебаний

2)  A(w) – амплитуда зависит от частоты воздействия. При разных частотах А(w) будет разной.

3)  j_о – разность фаз этого колебания и колебания вынужденного воздействия.

Амплитуда вынужденных колебаний. Явление резонанса.

1)  Низкие частоты: w существеннее меньше w_о.

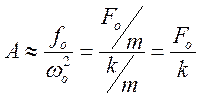 (на примере маятника)

При низкой частоте реакция на внешнее воздействие зависит от упругих свойств системы и от возвращающего воздействия. 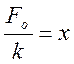 - статическое смещение

2)  Высокие частоты: w существеннее больше w_о.

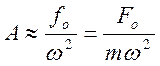 При высоких частотах определяющим является инертность системы. Чем больше инертность, тем амплитуда колебаний меньше.

3)  У зависимости А(w) должен быть максимум. Амплитуда максимальна, когда  минимальна.

w_о, b, f_o – const, мы их зафиксировали.

w₁=0

w₂=- резонансная частота.

Когда частота воздействия равна резонансной частоте, тогда будет максимум амплитуды.