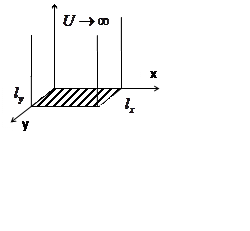
 Уравнение Шредингера:
Уравнение Шредингера: 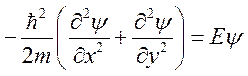 . Решение уравнения:
. Решение уравнения: ![]() . Получаем:
. Получаем: 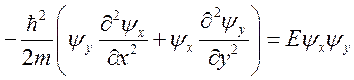 .
Разделим на
.
Разделим на ![]() :
: 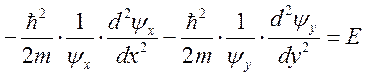 .
Можно записать 2 уравнения:
.
Можно записать 2 уравнения: 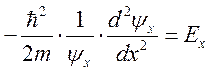 и
и 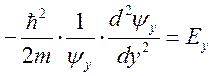 ,
, ![]() . Каждое
из них – это уравнение Шредингера для одномерной задачи. Следовательно,
. Каждое
из них – это уравнение Шредингера для одномерной задачи. Следовательно, ![]() и
и ![]() .
. ![]() ;
; ![]() .
Преобразуем решение в вид:
.
Преобразуем решение в вид: ![]() .
. ![]() и
и ![]() - это
условия 2-х стоячих волн (вдоль х и вдоль у).
- это
условия 2-х стоячих волн (вдоль х и вдоль у).
 Появляется 2 взаимно независимых
квантовых числа. Эти значения определяют вид
Появляется 2 взаимно независимых
квантовых числа. Эти значения определяют вид ![]() .
. 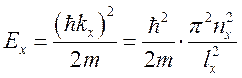 ;
; 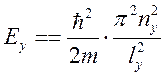 .
Отсюда получаем выражение для полной энергии частицы в двумерной яме:
.
Отсюда получаем выражение для полной энергии частицы в двумерной яме: 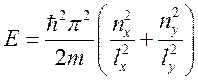 . Полная энергия оказывается квантована,
как и раньше. Значениям
. Полная энергия оказывается квантована,
как и раньше. Значениям ![]() ,
, ![]() соответствует низшее состояние частицы в
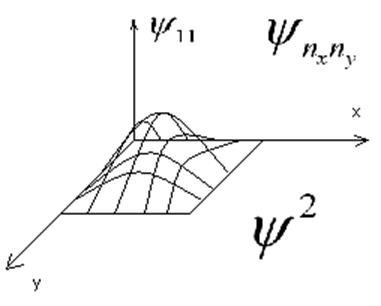
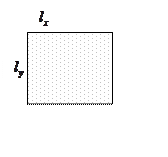
квантовой яме. На рисунке – функция
соответствует низшее состояние частицы в
квантовой яме. На рисунке – функция ![]() в яме.
в яме.
Вырождение состояний.
1. Общая
ситуация: ![]() , область прямоугольная.
, область прямоугольная.
 Если
Если 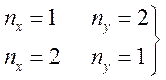
![]() . Для любой пары
квантовых чисел:
. Для любой пары
квантовых чисел: ![]() .
.
2. Если ![]() , т. е. два различных состояния (разные
волновые функции) обладают одной энергией. Такие состояния называются
вырожденными. Значения энергии тоже называются вырожденными значениями, или
вырожденными энергетическими уровнями. Вырождения появляются с появлением
симметрии. В 3-х мерном пространстве:
, т. е. два различных состояния (разные
волновые функции) обладают одной энергией. Такие состояния называются
вырожденными. Значения энергии тоже называются вырожденными значениями, или
вырожденными энергетическими уровнями. Вырождения появляются с появлением
симметрии. В 3-х мерном пространстве: ![]() .
Состояние будет однозначно описываться тройкой квантовых чисел
.
Состояние будет однозначно описываться тройкой квантовых чисел ![]() ,
, ![]() . Если
возьмем кубическую яму, то произойдет вырождение. Перестановка квантовых чисел
будет приводить к одинаковой энергии.
. Если
возьмем кубическую яму, то произойдет вырождение. Перестановка квантовых чисел
будет приводить к одинаковой энергии.
 Гармоническим
осциллятором называют частицу, совершающую одномерное движение под действием
квазиупругой силы
Гармоническим
осциллятором называют частицу, совершающую одномерное движение под действием
квазиупругой силы ![]() .Потенциальная энергия такой
частицы имеете вид
.Потенциальная энергия такой
частицы имеете вид 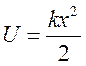 . Собственная частота
гармонического осциллятора равна
. Собственная частота
гармонического осциллятора равна ![]() , где m-масса частицы. Отсюда
, где m-масса частицы. Отсюда 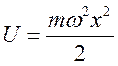 . В одномерном случае
. В одномерном случае ![]() . Поэтому уравнение Шрёдингера,
описывающее стационарные состояния осциллятора имеет вид
. Поэтому уравнение Шрёдингера,
описывающее стационарные состояния осциллятора имеет вид 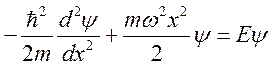 (2).
(2).
Волновые функции, характеризующие состояние частицы в одномерной бесконечно глубокой яме, и волновые функции квантового гармонического осциллятора имеют много общего: как у волновых функций, так и у плотности вероятности.
Однако
есть принципиальное различие, Двигаясь в бесконечно глубокой потенциальной
яме, частицы не могут выйти за пределы ямы. В случае осциллятора это
ограничение остается лишь для классической частицы. Ее координата не может
превышать величину амплитуды колебаний, то есть ![]() . В
точках
. В
точках ![]() происходит изменение движения частицы на
противоположное под действие возвращающей силы. Квантовая частица имеет
конечную вероятность оказаться в результате своего движения за пределами
квадратичной потенциальной ямы.
происходит изменение движения частицы на
противоположное под действие возвращающей силы. Квантовая частица имеет
конечную вероятность оказаться в результате своего движения за пределами
квадратичной потенциальной ямы.
Уравнение (2) имеет конечные, однозначные и непрерывные решения при значения параметра Е равных:
![]()
На рис.1
дана схема энергетических уровней гармонического осциллятора. Для наглядности
уровни вписаны в кривую потенциальной энергии. В отличие от классического
осциллятора спектр энергий получается квантованным. Величина полной энергии
определяется частотой ![]() и квантовым числом n.
и квантовым числом n.
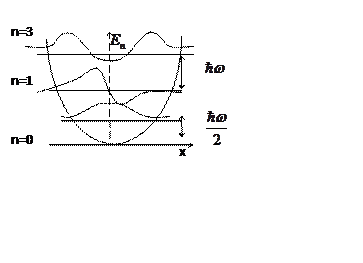
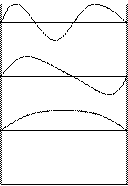
Гармонический осциллятор Яма с бесконечной энергией
Снизу
спектр энергий ограничивается значением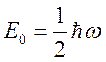 . Уровень, соответствующий этому
значению энергии, является основным уровнем осциллятора. Два любых соседних
уровня разделены одинаковым промежутком
. Уровень, соответствующий этому
значению энергии, является основным уровнем осциллятора. Два любых соседних
уровня разделены одинаковым промежутком ![]() . Такое
расположение уровней называется эквидестантным. Так как минимальное значение
энергии
. Такое
расположение уровней называется эквидестантным. Так как минимальное значение
энергии ![]() , то квантовый осциллятор в принципе не
может находиться в покое. Колебания осциллятора с энергией
, то квантовый осциллятор в принципе не
может находиться в покое. Колебания осциллятора с энергией ![]() называются нулевыми колебаниями. Их
существование непосредственно вытекает из принципа неопределенности. Если бы у
квантового осциллятора наблюдалось состояние покоя, то при этом частица
находилась в точке равновесия. О означает, что неопределенность ее координаты
называются нулевыми колебаниями. Их
существование непосредственно вытекает из принципа неопределенности. Если бы у
квантового осциллятора наблюдалось состояние покоя, то при этом частица
находилась в точке равновесия. О означает, что неопределенность ее координаты ![]() . Тогда неопределенность импульса
. Тогда неопределенность импульса ![]() , согласно принципу Гейзенберга, должна
стремиться к бесконечно большой величине. По этой причине осциллятор должен
обязательно обладать конечной (не равной нулю) энергией.
, согласно принципу Гейзенберга, должна
стремиться к бесконечно большой величине. По этой причине осциллятор должен
обязательно обладать конечной (не равной нулю) энергией.
Имеется
еще одно интересное свойство, связанное с изменение энергии квантового
осциллятора. Оказывается, существует определенное правило отбора, которое
ограничивает возможность изменения квантового числа n при переходе осциллятора из одного состояния в
другое. Согласно этому правилу n может изменяться только на
единицу:![]() .
Это означает, что энергия осциллятора может изменяться лишь порциями, равными
по величине
.
Это означает, что энергия осциллятора может изменяться лишь порциями, равными
по величине ![]() ( величина энергии фотона ). Частица,
переходя на более низкий уровень излучает фотон, а поглотив фотон с энергией,
необходимой для перехода на более высокий уровень, занимает его.
( величина энергии фотона ). Частица,
переходя на более низкий уровень излучает фотон, а поглотив фотон с энергией,
необходимой для перехода на более высокий уровень, занимает его.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.