Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 8

Заметим, что в результате наложения волн характер колебаний существенно изменился. Колебания во всех точках происходят одновременно с одинаковой частотой ω. Иными словами, вся система колеблется как целое, причем передачи энергии в процессе колебаний от одной точки к другой не происходит. Каждая частица колеблется так, как это происходит при обычных колебаниях — в момент времени, когда ее смещение максимально, максимальна ее потенциальная энергия и минимальна кинетическая, и наоборот. В каждый момент времени система частиц образует в пространстве периодическую структуру, форма которой определяется амплитудным множителем в выражении (3.61):
A(x) = 2u₀ coskx. В точках x = ±2nl/4 (n = 0, 1, 2,..)                                         (3.62)

амплитуда колебаний наибольшая, а в точках

x=±(2n+1)l/4                                                   (3.63)

она равна нулю. Эти точки называют соответственно пучностями и узлами волны. Узлы и пучности волны расположены друг от друга на расстоянии l/4.

Описанную картину колебаний во встречных бегущих волнах называют стоячей волной. Ясно, что в замкнутом объеме, где бегущая волна испытывает отражение от обеих границ, устанавливается стоячая волна.

19.Интерференция света от двух когерентных источников.

Интерференция света от двух источников.

Пусть есть два источника света, и они излучают на одной и той же частоте.

                           ○ в этой точке складываются два колебания с одинаковой частотой.

1      х₁

○

              х₂

       ○ 2          Е₀²=Е₁₀²+Е₂₀²+2Е₁₀*Е₂₀*cosΔφ, Δφ(t)≠const

I~E₀²

I=I₁+I₂+2√I₁*I₂ *cosΔφ

<I>=<I₁>+<I₂>+0

Если два источника не когерентны, то перераспределения не наблюдается. В случае когерентных источников сложение двух источников зависит от Δφ.

1.  Δφ=2πn

I=I₁+I₂+2√I₁*I₂   - условие max интерференции

Если I₁=I₂ , то I=4 I₁

2.  Δφ=π(2n+1)

I= I₁+I₂-2√I₁*I₂   - условие min интерференции

Если I₁=I₂ , то I=0

Е₁=Е₀₁cos(ωt-kx₁)

Е₂=Е₀₂cos(ωt-kx₂)

Δφ=φ₂- φ₁= kx₁- kx₂

Каждая волна может двигаться в своей среде, у которой свой коэффициент преломления.

Δφ=kx₁- kx₂=n₁*2π/λ₀*x₁-n₂*2π/λ₀*x₂=2π/λ₀(n₁x₁-n₂x₂)   x(s)-геометрический путь

                                                                                             nx(ns)-оптический путь

Δ= n₁x₁-n₂x₂=n₁s₁-n₂s₂

Оптическая разность хода волн зависит от положения точки в пространстве. Как результат, сложение волн в пространстве зависит от точки в пространстве.

1. max

Δφ=2πm, m=0,1…

2π/λ₀(n₁x₁-n₂x₂)= 2πm => Δ=mλ₀

2. min

      2π/λ₀*Δ=π(2m+1) => Δ=λ₀/2*(2m+1)

Существует множество других точек, где результат сложения волн даёт промежуточное значение интенсивности. В произвольной точке I_min≤I≤I_max

Max относительно центра располагаются симметрично.

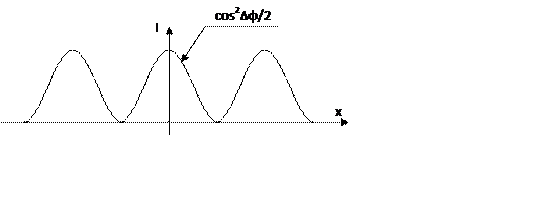
Δх_max=λ₀l/nd

Разрешение картины определяется двумя параметрами: длиной волны и отношением l/d.

По мере удаления Δφ растет и вектор Е поворачивается.

I=I₁+I₂+2√I₁*I₂ *cosΔφ=2I₀+2I₀cosΔφ=4I₀+

I~cos²(x)

Поскольку координаты max зависят от длины волны, то положение max для разных длин волн будут разные на экране. Если источники является источниками белого света, то на экране получится разложение в спектр.

20.Интерференция света от многих когерентных источников.

Интерференция света от многих источников.

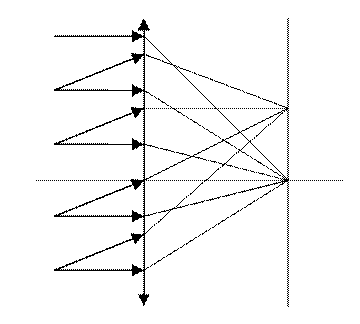Лучи, идущие под одним углом, собираются в одной и той же точке. Происходит сложение N электромагнитных волн. Результат сложения зависит от того с какими разностями фаз они приходят.

Е₀₁=Е₀₂=    … =Е₀.

 

В центр картины в главный фокус приходят волны в одной и той же фазе

Е=N*Е₀ => I=N²*I₀ – интенсивность в центре больше в N² раз.

Если мы уходим от центра, то лучи приходящие в некоторую точку имеют разность не равную нулю, у них появляется разность хода.

I=N²I₀cos²(Δφ/2)

Поскольку интенсивность зависит от Δφ, то у неё есть max и min значения. В картине распределения интенсивности выделяются главные и дополнительные min и max.