Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 13

 

Дифракция была обнаружена у электр. частиц, атомов и молекул.у них есть волновые свойства.

Длины волн де Бройля совпадали с дефракционной картиной.

Волновая функция

Де Бройль предполагает с частицами связывать некоторую волновую функцию.

Это уравнение плоской нармонической волны.

Какой смысл самой этой функции и её параметров?

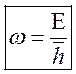1)  *2π  => =>   2)  =>

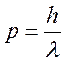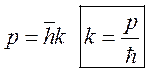
Частота зависит от энергии, волновое число от импульса. Если как обычно пуляем электрон, то вероятность, что он окажется на dS экрана dP=ψ²dV . 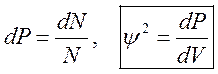 - плотность распределения вероятности. Условие нормировки волновой функции: 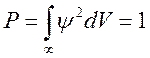. Частица хоть где-то, да находится.

Квантовая механика утверждает, что возможно лишь вероятностное описание движения частиц. Если получена  пси, то мы полностью описали движение. Понятия траектории для частиц нет. Электрон не кубик, даже в идеальных условиях не летит одинаково.

Принцип и соотношения неопределённостей

Состояние движения материальной точки полностью определено, если знаем её положение и скорость. С частицами – все не так. Пусть электрон заключен между двух стенок. Сжимаем стенки

   Δx-неопределённость координат

У реальной волновой функции нет определённой длины волны, но мы можем представить её в виде ряда Фурье, где каждое слагаемое имеет свой период. Реальная волновая функция характеризуется неопределённостью длины волны => неопределённостью импульса. На рисунке, что при уменьшении Δx, увеличивается Δp. Cам принцип: реальные состояния частиц таковы, что координата и импульс, связанные с одним и тем же направлением не могут быть одновременно точно определены. Зная Δx мы не можем узнать Δp.

Δx=nλ ,  =>  =>    =>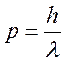        

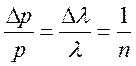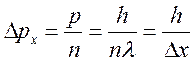В общем случае пси может быть не синусоидой, тогда слагаемых ряда Фурье больше и Δp больше.

   точное - 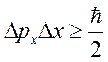 .   ΔE – неопределённость энергии состояния частицы, Δt –время жизни состояния частицы. .

29. Уравнение Шредингера. Квантово-механическое описание свободных частиц.

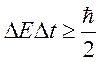Основная идея Шрёдингера состоит в том, чтобы математическую аналогию между геометрической оптикой и классической механикой перенести на волновые свойства света и частиц.

Получим уравнение Шрёдингера из выражения для волновой функции свободного электрона . Перепишем его в комплексной форме .

Используя связи частоты с энергией, а волнового числа с импульсом, получаем:   .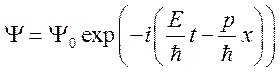

В общем случае  – полная энергия частицы,   , 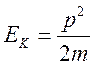   – кинетическая энергия и –энергия взаимодействия.

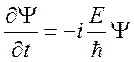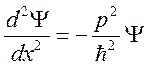Найдем первую производную по  и вторую по координате от ф-ции Y:       (1),    (2).

Домножим уравнение  (1)  на , а уравнение (2) на  (таким образом множители в правых частях  будут иметь размерность энергии):

, .

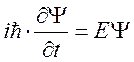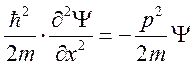Сложим полученные уравнения:

.

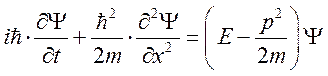Так как 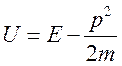, то последнее равенство перепишется в виде .

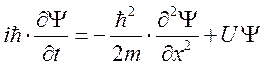Это и есть уравнение Шрёдингера. Оно получено для одной координаты . Если его переписать для 3 координат , то введя оператор Лапласа, окончательно будем иметь

.

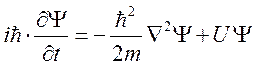Уравнение Шрёдингера нельзя непосредственно вывести из фундаментальных законов классической физики. Уравнение Шрёдингера позволяет находить волновую функцию в произвольный момент времени. Для этого надо знать волновую ф-цию в фиксированный момент времени, массу частицы и энергию взаимодействия частицы с силовым полем. Найденная волновая ф-ция дает возможность рассчитать вероятность нахождения частицы в произвольной точке пространства для любого момента времени.

Основные свойства, которым должны удовлетворять волновые функции – решения уравнения Шрёдингера:

1.  Волновая функция линейна, т.е. если …- решения уравнения, то их линейная комбинация 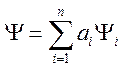– решение.

2.  Первые частные производные по координатам являются линейными

3.  Волновая функция и её пространственные производные должны быть однозначными, конечными и непрерывными.

4.  При стремлении  к ∞ значение волновой функции должно стремиться к нулю.

Уравнение Шрёдингера для стационарных состояний.