Пример 1.
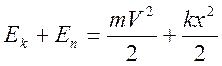
![]() =>
=>
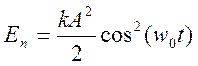
![]()
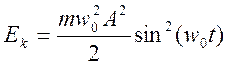
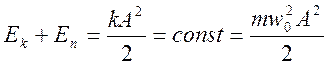
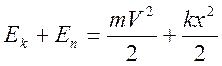 продифференцируем по x и получим
продифференцируем по x и получим ![]() .
.
Причины, по которым получается именно это уравнение:
1) система консервативна.
2) Энергия – квадратичная форма от смещения и скорости.
Для колебательного контура:
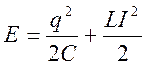
5.Осциллятор с трением. Дифференциальное уравнение осциллятора с рением. Режимы движения осциллятора с трением.
В реальных осцилляторах есть трение, трение трансформирует энергию колебаний во внутреннюю энергию. При достаточно большом трении колебаний может и не быть.
1.
 Колебательный
контур
Колебательный
контур
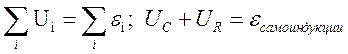 ;
;
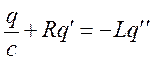 ;
;
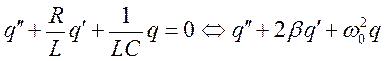
2. Пружинный маятник
 Пружинный маятник движется в
некоторой среде, тогда на маятник будет действовать сила сопротивления, модуль
которой
Пружинный маятник движется в
некоторой среде, тогда на маятник будет действовать сила сопротивления, модуль
которой ![]() .
.
![]()
![]() ;
;
![]() ;
; 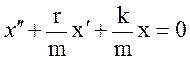
В общем случае дифференциальное уравнение осциллятора с трением:
(1)
![]() , где
, где ![]() -
квадрат собственной частоты,
-
квадрат собственной частоты, ![]() - коэффициент затухания.
- коэффициент затухания.
дифференциальное уравнение осциллятора с трением описывает собственную динамику осциллятора, у которого трение линейно зависит от скорости.
Режимы осциллятора с трением
Характер движения осциллятора с трением. Если трение очень маленькое, то колебания должны быть, но их амплитуда должна падать. Если трение велико, то колебаний может не быть.
Решение (1) будем искать в виде x=Aegt.
![]()
Aegt (g2+2bg+![]() )=0
)=0
g2+2bg+![]() =0
=0
g1,2=![]()
Возможны
три ситуации, связанные с коэффициентами ![]() и
и ![]() , и они соответствуют трем возможным
режимам осциллятора с трением:
, и они соответствуют трем возможным
режимам осциллятора с трением:
1.
Апериодический
режим ![]() >
>![]()
g1<0, g1<0
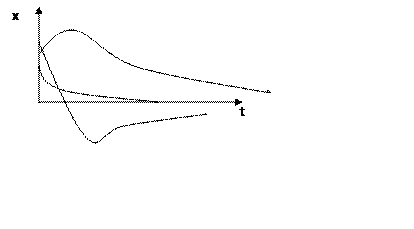 x(t)= A1eg1t+ A2eg2t= A1e(
x(t)= A1eg1t+ A2eg2t= A1e(![]() )*t+ A2e(
)*t+ A2e(![]() )*t
)*t
Апериодический режим возникает при большом трении в системе.
2. Режим критического затухания.
b=![]()
g1=g2=-b
x(t)=(A+Bt)e-bt
Вид картины такой же.
В режиме критического затухания система наиболее быстро возвращается в положение равновесия среди апериодических режимов.
Коэффициент сопротивления r называется критическим коэффициентом затухания, b – коэффициент критического затухания, R- критическое сопротивление контура.
Найдем выражение для критического сопротивления:
bкр= ![]() ;
; 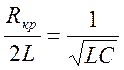 ;
; 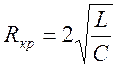
3. Режим затухающих колебаний.
b< ![]() ;
g1,2=
;
g1,2=![]() ,
где
,
где ![]()
![]()
x(t)=Re(![]() (t))= A1e-btcos(wt+j01)+ A2e-btcos(wt+j02)= A0e-btcos(wt+j0)
(t))= A1e-btcos(wt+j01)+ A2e-btcos(wt+j02)= A0e-btcos(wt+j0)
A0 – зависит от энергии.
j0 – зависит от начального состояния системы.
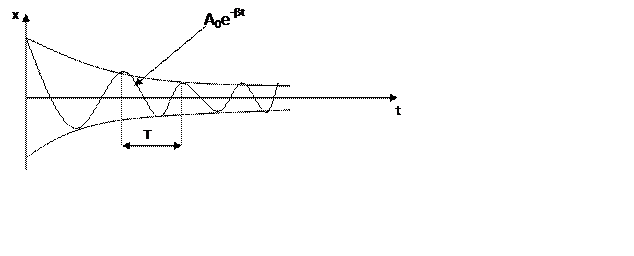
 b<
b< ![]()
![]() x(t)=
A0e-btcos(wt+j0)
x(t)=
A0e-btcos(wt+j0)
 |
Положим j0=0.
Колебания не периодичны (т.к. max не повторяются), но они характеризуются периодом затухающих колебаний.
T=![]() ,
, ![]() -
зависит не только от возвращающего воздействия, но и от трения.
-
зависит не только от возвращающего воздействия, но и от трения.
![]() -
постоянная времени затухания(времени релаксации) – за это время
амплитуда уменьшается ровно в e раз.
-
постоянная времени затухания(времени релаксации) – за это время
амплитуда уменьшается ровно в e раз. ![]() ; A=A0e-1;
; A=A0e-1; ![]() =1; b=
=1; b=![]()
d - логарифмический декремент затухания.
d=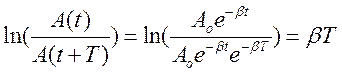 , d=
, d=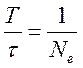
d обратно числу колебаний, в течении которых амплитуда уменьшается в e раз.
6.Затухающие колебания осциллятора и их характеристики. Энергия затухающих колебаний. Добротность осциллятора.
Если на
материальную точку массой ![]() ,
кроме упругой силы
,
кроме упругой силы ![]() ,
действует еще мила трения
,
действует еще мила трения ![]() ,
где
,
где ![]() -
коэффициент трения и
-
коэффициент трения и ![]() -
скорость колеблющейся точки, то колебания точки будут затухающими. Уравнение
затухающего колебательного движения имеет вид
-
скорость колеблющейся точки, то колебания точки будут затухающими. Уравнение
затухающего колебательного движения имеет вид ![]() , где
, где ![]() - коэффициент затухания. При
этом
- коэффициент затухания. При
этом ![]() и
и
![]() ,
где
,
где ![]() -
круговая частота собственных колебаний. Величина
-
круговая частота собственных колебаний. Величина ![]() называется логарифмическим
декрементом затухания.
называется логарифмическим
декрементом затухания.
4. Режим затухающих колебаний.
b< ![]() ;
g1,2=
;
g1,2=![]() ,
где
,
где ![]()
![]()
x(t)=Re(![]() (t))= A1e-btcos(wt+j01)+ A2e-btcos(wt+j02)= A0e-btcos(wt+j0)
(t))= A1e-btcos(wt+j01)+ A2e-btcos(wt+j02)= A0e-btcos(wt+j0)
A0 – зависит от энергии.
j0 – зависит от начального состояния системы.
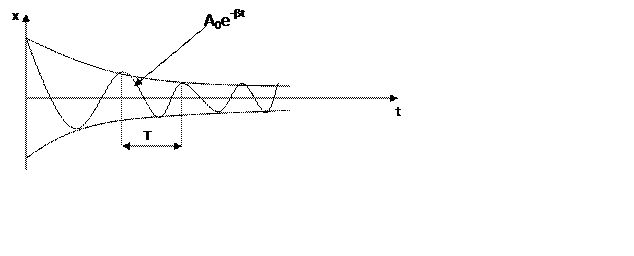
 b<
b< ![]()
![]() x(t)=
A0e-btcos(wt+j0)
x(t)=
A0e-btcos(wt+j0)
 |
Положим j0=0.
Колебания не периодичны (т.к. max не повторяются), но они характеризуются периодом затухающих колебаний.
T=![]() ,
, ![]() -
зависит не только от возвращающего воздействия, но и от трения.
-
зависит не только от возвращающего воздействия, но и от трения.
![]() -
постоянная времени затухания(времени релаксации) – за это время
амплитуда уменьшается ровно в e раз.
-
постоянная времени затухания(времени релаксации) – за это время
амплитуда уменьшается ровно в e раз. ![]() ; A=A0e-1;
; A=A0e-1; ![]() =1; b=
=1; b=![]()
d - логарифмический декремент затухания.
d=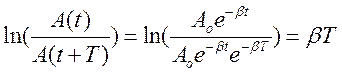 , d=
, d=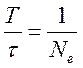
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.