Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 9

1. главный max

I=N²I₀,   Δφ=0  =>  Δφ=2πm, m=0,1,2…

Величина m называется порядком главного max. Количество max слева и справа от центрального должно быть одинаково.

2. главный min

I=0    N*Δφ=mπ, m=1,2…

N*Δφ=2πm

21.Интерференция света на тонких пленках.

22.Принцип Гюйгенса-Френеля. Метод зон Френеля.

Гюйгенс предложил принцип, позволяющий объяснить явление дифракции.

Идея: каждая точка пространства, до которой дошел волновой процесс становится слабым источником вторичных волн. Если среда однородная, то эти волны сферические, но распространяются в переднюю полусферу. Принцип Гюйгенса позволил качественно объяснить дифракцию, но не давал возможности рассчитать распределение энергии. Френель усовершенствовал принцип и превратил его в метод расчета распределения энергии.

Идея: вторичные волны являются когерентными и как следствие они интерферируют. Можно использовать принцип суперпозиции волн.

23.Дифракция света на щели.

(**)

1. min: bsinα=mλ в щели укладывается четное количество зон Френеля
2. max: bsinα=(2m+1)λ/2

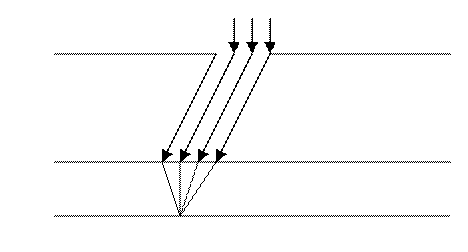
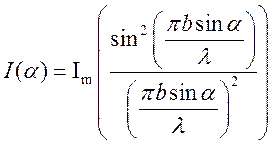sinα=λ/2:

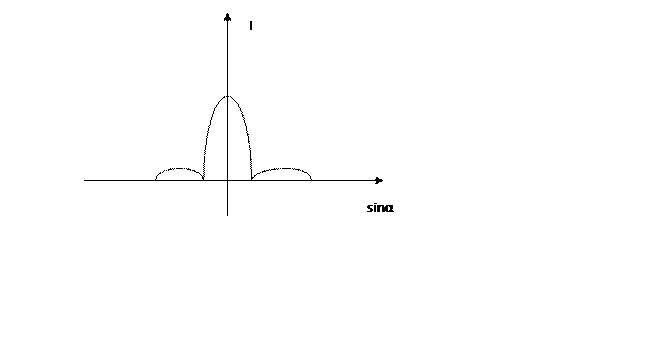
Выражаем порядок минимума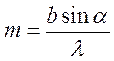

Максимальный порядок минимума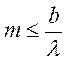

1. Если b уменьшается, то расширяется центральный максимум, так как минимумы удаляются их количество становится меньше.
2. если b<λ, то минимумы находятся на бесконечности и их вообще нет. Это условие исчезновения минимума.

С уменьшением щели сам max становится меньше, так как все меньше энергии проникает в щель.

Положение минимумов и максимумов зависит от длины щели.

24.Дифракция света на решетке.

Решетка – это совокупность одинаковых параллельных щелей.

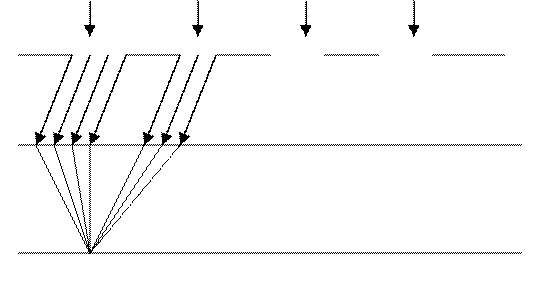
Всего щелей N

Здесь происходит интерференция: (***)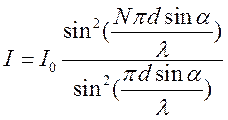

I(α)=Im(**)(***)

(**) – дифракция на одной щели

(***) – интерференция от N источников.

1. Условие главных минимумов:

Главные минимумы соответствуют минимальной дифракции на одной щели:

bsinα=mλ

I щели ≡ 0

2. Условие главных максимумов:

Когда волны от соседних щелей приходят в фазе, то будет наблюдаться максимум:

dsinα=mλ

период решетки         разность хода2-х

                                   соседних волн

Это условие может совпадать с 1- ым если d кратно b.

3. Дополнительные min:

Ndsinα=mλ

4. Дополнительные max:

разность хода 1-го и последнего источника должна быть кратна нечетному количеству λ/2

Ndsinα=(2m+1)λ/2

Дифракционная решетка:

Для любой решетки оказывается более изрезанной по сравнению с щелью. На ней наблюдается большее количество соседних щелей. Максимумы в итоге становятся уже.

Если пропускать белый свет, то решетка дает разложение в спектр.

Дифракционная решетки используется для определения длины света.

Чем меньше ширина щели, тем больше точность измерения.

25.Поляризованный свет. Способы получения поляризованного света.

Естественный и поляризованный свет.

Свет, с волновой точки зрения – это электромагнитная поперечная волна. С течением времени вектор Е случайным образом меняет своё направление. В естественном свете нет выделенного направления колебания вектора Е, т.е. плоскость колебания вектора Е меняется хаотически. Такое явление связанно с процессом излучения света веществом, где каждый атом вещества излучает случайным образом. Если в свете обнаруживается закономерность в поведении плоскости колебания вектора Е, то свет называется поляризованным. Естественный свет не поляризованный.

Примеры поляризованного света:

1.плоскополяризованный: колебание светового вектора Е происходит в одной плоскости. Эта плоскость называется плоскостью колебаний светового вектора.   

   Е    

 ←○→

2.эллиптически поляризованный свет:

Световой вектор вращается равномерно либо по часовой, либо     против часовой стрелки и конец вектора описывает эллипс.

Е2