Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 34

Наличие единицы в данном выражении отмечает тот факт, что система С рассматривается в интересующем нас единственном состоянии. Обозначим полное число доступных состояний замкнутой макросистемы  и отметим, что в состоянии термодинамического равновесия эта величина будет константой: . Из всех доступных состояний  только в состояниях  система С находится в квантовом состоянии с энергией ε_i. Исходя из того что все доступные состояния равновероятны, получаем вероятность обнаружения системы С в квантовом состоянии с энергий ε_i:

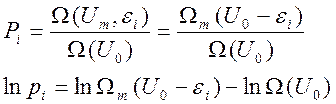
Учитывая, что U₀>>>ε_i (условие термостата), разложим  в ряд Тейлора и ограничимся первыми двумя членами

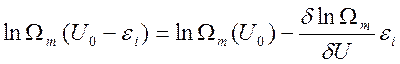
Тогда

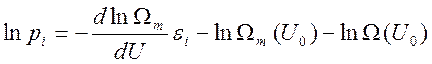
Производная 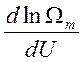 вычисляется при постоянном числе частиц и постоянном объеме и соответствует определению температуры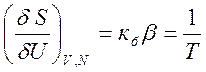. Второе слагаемое, как и последнее, являются константами, так как U₀ = const.

В этом случае формула (4.51) примет вид

Откуда

Постоянная А в последней формуле определяется из условия нормировки:

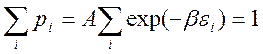
где суммирование ведется по всем квантовым состояниям. С учетом нормировки получаем                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                       

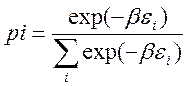
Распределение вероятностей по состояниям, описываемое вышеуказанной формулой, носит название канонического распределения. Знание вероятностей различных состояний системы само по себе не имеет особого значения. На практике гораздо важнее предсказать значения наблюдаемых физических величин. Вычислить их можно, используя правила теории вероятностей. Обозначим f(ε) некоторую физическую величину, которая является функцией энергии. Тогда ее среднее значение < f > будет определяться по формуле

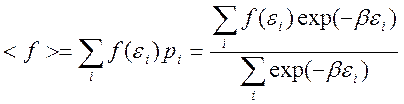
В частности, средняя энергия системы

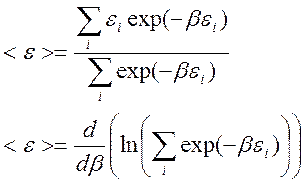
Для вычисления средней энергии предпочтительна последняя формула, так как в ней требуется только один раз провести суммирование. Поэтому сумма 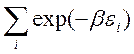 имеет самостоятельное значение и носит название статистической суммы

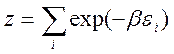
43.Большое каноническое распределение Гиббса. 44.Распределение Ферми-Дирака.

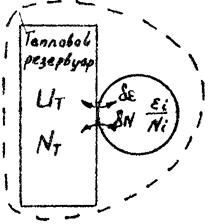Рассмотрим систему, которая обменивается с термостатом не только энергией, но и частицами (см. рис.). Т.е. система С находится в диффузионном контакте с термостатом. Пусть система С и термостат являются замкнутой макросистемой:

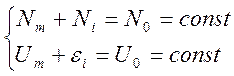
Условие замкнутости необходимо дополнить неравенствами

,

которые обусловлены определением термостата как системы, обладающей огромной энергией U_m  огромным числом частиц N_m.

Индексом i обозначено квантовое состояние, в котором находится N_i частиц с полной энергией ε_i.

Вычислим вероятность обнаружения системы С в i-м квантовом состоянии. Обозначим через  число доступных состояний термостата с энергий U_T и числом частиц N_m. Тогда число доступных состояний замкнутой макросистемы, когда система С находится в i-м квантовом состоянии, определится формулой

Полное число доступных состояний замкнутой макросистемы  в условиях равновесия. В этом случае искомая вероятность определяется отношением

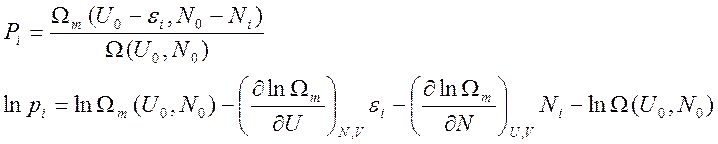
Учитывая, что

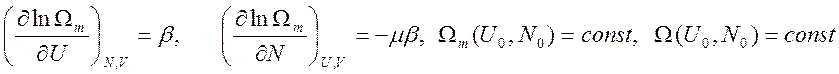
получаем

или

где  в формуле. Константа А определяется из условия нормировки

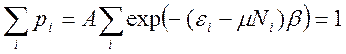
Сумма по всем квантовым состояниям системы С называется большой статической суммой

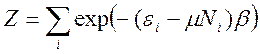
Окончательно, большое каноническое распределение примет вид

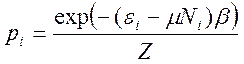
С помощью большого канонического распределения вычисляются наблюдаемые средние и, в частности, среднее число частиц в системе С

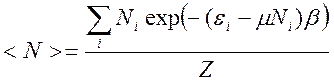
Легко убедиться, проведя дифференцирование, в том, что