Гармонические колебания. Характеристики и формы представления. Сложение однонаправленных колебаний. Векторные диаграммы. Гармонические осцилляторы. Уравнение состояния идеального газа, страница 32

 - энтропия – величина, равная натур. Логарифму от степени вырождения макр-мы. Степень вырождения макр-ния макр-мы связана со степенью разупорядоченности макр-мы, т.е. со степенью беспорядка в ней. Чем выше степень вырождения, тем больше беспорядок (хаос) в макр-ме => энтропия – мера беспорядка. В классической термодинамике также используется понятие энтропии: S=klng, где K – пост. Больцмана. . Условием равновесия макр-м, находящихся в тепл. Контакте, является равенство скоростей изменения энтропии макр-м по энергии (физич. смысл производной).

5 Свойства энтропии.

1) при понижении темп-ры движение частиц, образующих любую макр-му, замедляется. Это значит: понижение темп-ры снижает хаотичность поведения частиц макр-мы. Это означает: снижение темп-ры макр-мы вызывает уменьшение её энтропии =>если темп-ра стремится к 0, то σ→min. Конкретное значение σ в наинизшем квантовом состоянии макр-мы зависит от ст-ни вырождения этого состояния. Если ст-нь вырождения = 1 => σ_min=0. стремление σ к минимальному значению при снижении темп-ры называю третьим началом термодинамики.  2) аддитивность термодинамики. Пусть существуют 2 макр-мы, которые между собой не контактируют. Каждая из них находится в равновесном состоянии. Ст-нь вырождения 1ой системы =g₁, 2ой – g₂. Т.к. каждому из g₁ микр-ний 1ой может соответствовать любое из g₂ микр-ний второй системы, то ст-нь вырождения объединённой системы: ;  ;  - энтропия объединённой макр-мы=сумме энтропий макр-м, образующих её. 3) второе начало термодинамики (стремление энтропии к возрастанию). Пусть существуют 2 макр-мы. Каждая находится в равновесном состоянии. В начальном состоянии они имеют g_1нач и g_2нач . У объединённой системы в начальном состоянии: g_1нач*g_2нач. Пусть между макр-мами возник тепловой контакт. Объед-ная макр-ма окажется в неравновесном состоянии. Согласно постулатам, она должна перейти в новое равновесное состояние. g равновесного состояния всегда > g неравновесного => g_1нач*g_2нач≤ g_1кон*g_2кон. Взяв логарифм: σ_нач ≤σ_кон – конечная энтропия макр-мы не м. быть меньше начальной. => в результате естественных процессов, самопр-но идущих в макр-ме, энтропия может только возрастать. Самопроизвольное уменьшение энтропии системы невозможно. 2ое начало терм-ки позволяет определить, в каком направлении могут происходить самопроизвольные процессы в макр-ме. Эти процессы всегда идут так, что энтропия системы возрастает. При тепловом контакте энергия сампр-но передаётся от системы с большей темп-рой системе с меньшей. Пример: если открыть вентиль в баллоне со сжатым газом, он выйдет. Газ, занимающий больший объём, рассредоточен сильнее, чем газ в малом объёме. Выход газа из баллона означает увеличение его энтропии. Обратный процесс (газ в баллон) невозможен. Замечание:  2ое начало терм-ки не запрещает самопр-ное уменьшение энтропии у какой-то части макр-мы. Но 2ое начало указывает: уменьшение σ в одной части обязательно приведёт к росту σ в др. части. Рост σ в др. части не может быть меньше убывания σ в первой части. Суммарная σ не может уменьшиться. Флюктуация – самопроизвольное изменение энтропии части макр-мы.

5.1 Диффузионный контакт макросистем.

Диффузионным контактом называется контакт, при котором системы могут обмениваться частицами, из которых они состоят. Рассмотрим случай, когда системы могут обмениваться как частицами так и энергией. Пусть есть две макросистемы: первая состоит из  частиц, вторая – из . Полное число частиц: N=+. Система изолирована от внешнего мира, поэтому N=const. Т.к. частицы могут переходить из одной системы в другую, то  и  переменные. Пусть системы находятся в однородном магнитном поле. Из-за этого они обладают энергиями  и .Общая энергия U=+, где U=const. Т.к. системы могут обмениваться энергиями, то  и  - переменные. После возникновения контакта между системами начинается обмен частицами и энергией. Следовательно объединенная система перейдет в равновесное состояние. В этом состоянии степень вырождения объединенной макросистемы будет максимальна. Следовательно dg=0. (дифференциал от степени вырождения равен нулю). Т.к. любому из  состояний первой системы может соответствовать любое из  состояний второй системы => степень вырождения объединенной макросистемы: g=*.  и  являются функциями числа частиц и энергии макросистемы. Полный дифференциал степени вырождения объединенной макросистемы: . (В равновесном состоянии = 0). Т.к. N=const => dN=0 => d=-d. dU=0 => d=-d, получим: . Перегруппируем слагаемые: . Т.к. d и d не равны нулю, то равенство выполняется если скобки равны нулю. Условие равновесия систем, находящихся в диффузионном контакте: 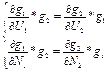. Разделим оба выражения на *, получим 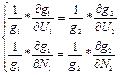 =>  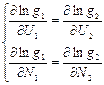=> 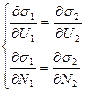. Это условие означает, что в равновесном состоянии  (температуры первой и второй систем одинаковы). Возможность обмена частицами вызвало появление еще одного условия. Это условие гласит, что при диффузионном контакте равновесие возникает, если скорость изменения энтропии по числу частиц у макросистем оказывается одинаковой.